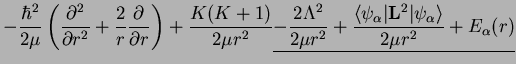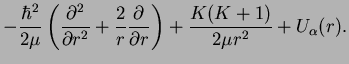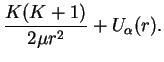Next: Radial SE
Up: Angular Momentum
Previous: Angular Momentum
Contents
Index
This is the simplest case. The total angular momentum of the nuclei is then
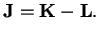 |
|
|
(1.16) |
Since we have neglected geometric phase terms, we can replace
 by its expectation value in the electronic state
by its expectation value in the electronic state
 under consideration,
under consideration,
This allows one to express everything in terms of total angular quantum numbers
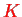 as follows:
We first write
as follows:
We first write
First,
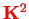 is conserved and can be replaced by its eigenvalue
is conserved and can be replaced by its eigenvalue
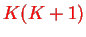 whence
whence
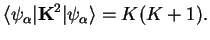 |
|
|
(1.20) |
Second,
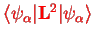 only depends on the electronic degrees of freedom and can therefore be simply added to the potential
only depends on the electronic degrees of freedom and can therefore be simply added to the potential
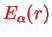 .
.
Finally, we assume that the electronic state
 is an eigenstate of the
is an eigenstate of the
 component
component
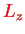 with eigenvalue
with eigenvalue
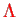 of the electronic angular momentum. Then,
of the electronic angular momentum. Then,
On the other hand, we have
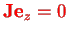 since the angular momentum of the two nuclei is perpendicular to the molecule axis
since the angular momentum of the two nuclei is perpendicular to the molecule axis
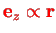 , thus
, thus
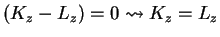 |
|
|
(1.22) |
and
Summarizing, we now have for the radial part
Thus we have finally arrived at the form for the effective potential energy,
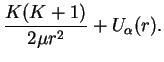 |
|
|
(1.24) |
The first term
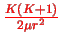 is the centrifugal energy as in the hydrogen problem.
Since
is the centrifugal energy as in the hydrogen problem.
Since
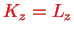 with fixed eigenvalue
with fixed eigenvalue
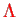 for the given state
for the given state
 , the eigenvalues of the total angular momentum must fulfill
, the eigenvalues of the total angular momentum must fulfill
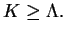 |
|
|
(1.25) |





Next: Radial SE
Up: Angular Momentum
Previous: Angular Momentum
Contents
Index
Tobias Brandes
2005-04-26
![]() is an eigenstate of the
is an eigenstate of the
![]() component
component
![]() with eigenvalue
with eigenvalue
![]() of the electronic angular momentum. Then,
of the electronic angular momentum. Then,