




Next: Spin
Up: Vibrations and Rotations in
Previous: Born-Oppenheimer Approximation
Contents
Index
Neglecting the geometric phase terms, Eq. (E.5.2), we have in three spatial dimensions
where
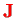 is the relative angular momentum operator of the nuclei. We have a three-dimensional problem which however due to the radial symmetry of
is the relative angular momentum operator of the nuclei. We have a three-dimensional problem which however due to the radial symmetry of
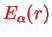 is reduced to a one-dimensional radial eqaution, very much as for the case of the hydrogen atom!
We could write the eigenfunctions of
is reduced to a one-dimensional radial eqaution, very much as for the case of the hydrogen atom!
We could write the eigenfunctions of
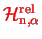 as
as
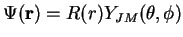 |
|
|
(1.14) |
with the corresponding angular quantum numbers
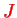 and
and
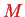 of the nuclear relative motion separated off in the spherical harmonics.
of the nuclear relative motion separated off in the spherical harmonics.
Instead of dealing with the angular momentum operator of the nuclei, one would rather descrive rotations of the whole molecule by the total angular momentum
 of the molecule
of the molecule
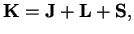 |
|
|
(1.15) |
where
 is the total angular momentum of all electrons and
is the total angular momentum of all electrons and
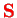 is the total spin.
is the total spin.
Subsections





Next: Spin
Up: Vibrations and Rotations in
Previous: Born-Oppenheimer Approximation
Contents
Index
Tobias Brandes
2005-04-26
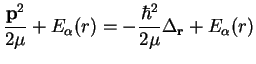
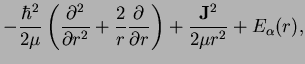
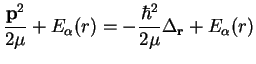
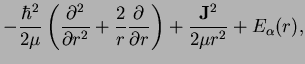
![]() of the molecule
of the molecule