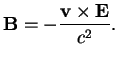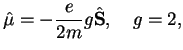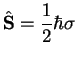Spin-Orbit Coupling in Atoms

In the hydrogen atom, the magnetic moment 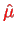$\hat{\bf\mu}$ of the electron interacts with the magnetic field 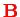${\bf B}$ which the moving electron experiences in the electric field 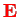${\bf E}$ of the nucleus,

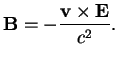$${\bf B} = -\frac{{\bf v} \times {\bf E}}{c^2}.$$ (3.8)

One has

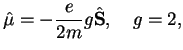$$\hat{\bf\mu} = -\frac{e}{2m}g\hat{\bf S},\quad g=2,$$ (3.9)

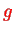where $g$ is the g-factor of the electron and

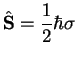$$\hat{\bf S} = \frac{1}{2}\hbar {\bf\sigma}$$ (3.10)

is the electron spin operator. Therefore,

$$-{\bf v} \times {\bf E} = {\bf v} \times {\bf\nabla} \frac{Ze}{4\pi \varepsilon_0 r} = {\bf... ...i \varepsilon_0 r} = \frac{1}{m} \hat{\bf L} \frac{Ze}{4\pi \varepsilon_0 r^3},$$ (3.11)

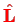where $\hat{\bf L}$ is the orbital angular momentum operator. This is reduced by an additional factor of 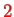$2$ (relativistic effects) such that

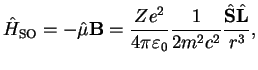$$\hat{H}_{\rm SO} = -\hat{\bf\mu} {\bf B}= \frac{Ze^2}{4\pi\varepsilon_0}\frac{1}{2m^2c^2}\frac{\hat{\bf S}\hat{\bf L}}{r^3},$$ (3.12)

which introduces a coupling term between spin and orbital angular momentum. Note that Eq. (II.3.12) can directly been derived by inserting Eq. (II.3.11) as ${\bf E} \times {\bf v} =-{\bf v} \times {\bf E}$ into Eq. (II.3.6).