




Next: Properties of Spin-Singlets and
Up: 2-Fermion Systems
Previous: 2-Fermion Systems
Contents
Index
Two Electrons
Electrons have spin
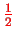 and we now have to work out how the electron spin enters into the Slater determinants. The single particle wave functions for particle
and we now have to work out how the electron spin enters into the Slater determinants. The single particle wave functions for particle
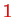 are products of orbital wave functions and spin wave functions,
are products of orbital wave functions and spin wave functions,
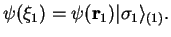 |
|
|
(2.2) |
For spin-
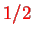 , the spin label
, the spin label
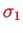 can take the two values
can take the two values
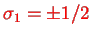 which by convention are denoted as
which by convention are denoted as
 and
and
 . The two spinors have the following representation in the two-dimensional complex Hilbert space (spin-space),
. The two spinors have the following representation in the two-dimensional complex Hilbert space (spin-space),
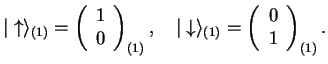 |
|
|
(2.3) |
Here, the index
 means that this spin referes to particle
means that this spin referes to particle
 .
.
We now consider the four possibilities for the spin projections
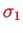 and
and
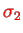 and the corresponding four sets of basis wave functions,
and the corresponding four sets of basis wave functions,
Here,
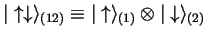 |
|
|
(2.5) |
is a product spinor, i.e. a spin wave function with particle (1) with spin up and particle (2) with spin down, and corresp[ondingly for the other product spinor.
We can now re-write the basis states Eq. (III.2.4) by forming linear combinations of the `mixed' spinors (exercise: check these !),
Here, the symmetric and antisymmetric orbital wave functions are defined as
Furthermore, the spin wave functions are defined as
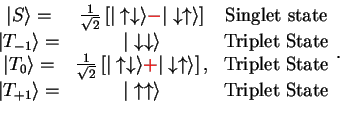 |
|
|
(2.12) |





Next: Properties of Spin-Singlets and
Up: 2-Fermion Systems
Previous: 2-Fermion Systems
Contents
Index
Tobias Brandes
2005-04-26
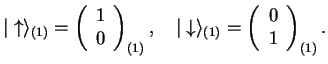
![]() and
and
![]() and the corresponding four sets of basis wave functions,
and the corresponding four sets of basis wave functions,
![$\displaystyle \frac{1}{\sqrt{2}}\left[ \psi_{\nu_1}( {\bf r}_1)\psi_{\nu_2}( {\bf r}_2)
+ \psi_{\nu_1}( {\bf r}_2)\psi_{\nu_2}( {\bf r}_1)
\right]$](img411.png)
![$\displaystyle \frac{1}{\sqrt{2}}\left[ \psi_{\nu_1}( {\bf r}_1)\psi_{\nu_2}( {\bf r}_2)
- \psi_{\nu_1}( {\bf r}_2)\psi_{\nu_2}( {\bf r}_1)
\right].$](img413.png)