




Next: Perturbation Theory
Up: The Exchange Interaction
Previous: The Exchange Interaction
Contents
Index
We assume a Hamiltonian for two identical electrons of the form
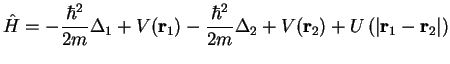 |
|
|
(2.17) |
which does not depend on the spin. The Hamiltonian is symmetric with respect to the particle indices 1 and 2.
The solutions of the stationary Schrödinger equation
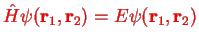 for the orbital parts of the wave function can be classified into symmetric and anti-symmetric with respect to swapping
for the orbital parts of the wave function can be classified into symmetric and anti-symmetric with respect to swapping
 and
and
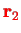 : this is because we have
: this is because we have
which means that the permutation operator
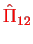 commutes with the Hamiltonian. The eigenstates of
commutes with the Hamiltonian. The eigenstates of
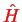 can therefore be chosen such they are also simultaneous eigenstates of
can therefore be chosen such they are also simultaneous eigenstates of
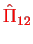 which are symmetric and antisymmetric wave functions with respect to swapping
which are symmetric and antisymmetric wave functions with respect to swapping
 and
and
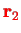 .
.
Since the total wave function (orbital times spin) must be antisymmetric, this means that for energy levels corresponding to symmetric orbital wave functions lead to spin singlets with total spin
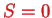 . Energy levels corresponding to anti-symmetric orbital wave functions lead to spin triplets with total spin
. Energy levels corresponding to anti-symmetric orbital wave functions lead to spin triplets with total spin
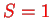 . Even though there is no spin-dependent interaction term in the Hamiltonian, the spin and the possible energy values are not independent of each other!
. Even though there is no spin-dependent interaction term in the Hamiltonian, the spin and the possible energy values are not independent of each other!





Next: Perturbation Theory
Up: The Exchange Interaction
Previous: The Exchange Interaction
Contents
Index
Tobias Brandes
2005-04-26
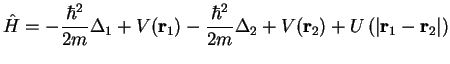
![]() . Energy levels corresponding to anti-symmetric orbital wave functions lead to spin triplets with total spin
. Energy levels corresponding to anti-symmetric orbital wave functions lead to spin triplets with total spin
![]() . Even though there is no spin-dependent interaction term in the Hamiltonian, the spin and the possible energy values are not independent of each other!
. Even though there is no spin-dependent interaction term in the Hamiltonian, the spin and the possible energy values are not independent of each other!