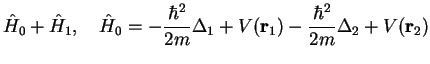 |
|||
| (2.19) |
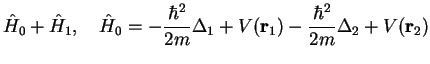 |
|||
| (2.19) |
![$\displaystyle \frac{1}{\sqrt{2}}\left[\phi_{\alpha}({\bf r}_1)
\phi_{\beta}({\bf r}_2) \pm \phi_{\alpha}({\bf r}_2) \phi_{\beta}({\bf r}_1) \right],$](img455.png) |
(2.20) |
We assume the single particle levels to be non-degenerate. Still, the two-electron level
![]() is degenerate because it corresponds to the two states
is degenerate because it corresponds to the two states
![]() (
(
![]() for the symmetric and
for the symmetric and
![]() for the anti-symmetric state. The corresponding two-by-two matrix of
for the anti-symmetric state. The corresponding two-by-two matrix of
![]() we need diagonalise for the degenerate first order perturbation theory in the sub-space spanned by
we need diagonalise for the degenerate first order perturbation theory in the sub-space spanned by
![]() is however diagonal so that things become easy:
is however diagonal so that things become easy:
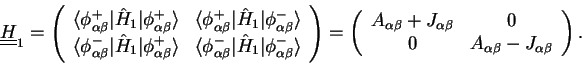 |
(2.21) |
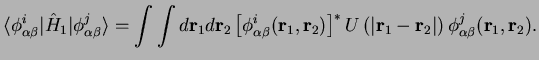 |
(2.22) |
Exercise: Show that
![]() .
.
The explicit calculation of the remaining diagonal elements
![]() and
and
![]() yields
yields
Exercise: Verify these expressions.
The symmetrical orbital wave function (
![]() ) belongs to the
) belongs to the
![]() (singlet) spinor, whereas the anti-symmetrical orbital wave function (
(singlet) spinor, whereas the anti-symmetrical orbital wave function (
![]() ) belongs to the
) belongs to the
![]() (triplet) spinors. Therefore, the unperturbed energy level
(triplet) spinors. Therefore, the unperturbed energy level
![]() splits into two levels
splits into two levels
| (2.25) | |||
| (2.26) |