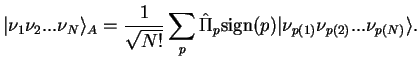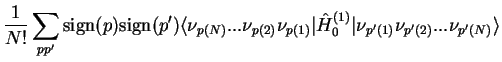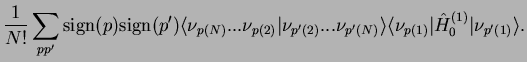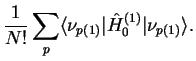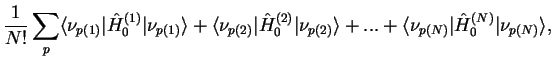Next: Expectation value of
Up: Hamiltonian for Fermions
Previous: Hamiltonian for Fermions
Contents
Index
Let us consider a
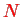 -Fermion state (Slater determinant), cf. Eq. (III.1.24),
-Fermion state (Slater determinant), cf. Eq. (III.1.24),
We wish to calculate the expectation value
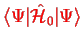 with
with
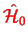 from
Eq. (IV.2.1). Consider for example the free Hamiltonian
from
Eq. (IV.2.1). Consider for example the free Hamiltonian
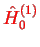 for the first particle,
for the first particle,
For
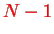 numbers we must have
numbers we must have
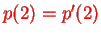 ,...,
,...,
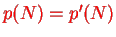 (otherwise the term is zero), but if you have a permutation with
(otherwise the term is zero), but if you have a permutation with
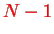 terms fixed, the last term ist automatically fixed and we have
terms fixed, the last term ist automatically fixed and we have
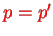 , thus
(note
, thus
(note
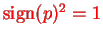 )
)
The sum of the single-particle Hamiltonians yields
but all the Hamiltonians
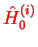 have the same form, the sum
have the same form, the sum
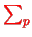 just gives
just gives
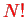 identical terms, and therefore
identical terms, and therefore
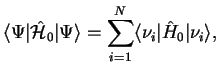 |
|
|
(2.5) |
where we can omit the index
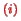 in
in
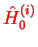 and write
and write
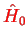 for the free Hamiltonian of a single particle (note that
for the free Hamiltonian of a single particle (note that
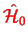 in Eq. (IV.2.1) is the total free Hamiltonian; some books use
in Eq. (IV.2.1) is the total free Hamiltonian; some books use
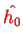 instead of
instead of
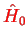 to make this distinction clearer, but small letters are not nice as a notation for a Hamiltonian).
to make this distinction clearer, but small letters are not nice as a notation for a Hamiltonian).





Next: Expectation value of
Up: Hamiltonian for Fermions
Previous: Hamiltonian for Fermions
Contents
Index
Tobias Brandes
2005-04-26