




Next: Explicit Calculation of ,
Up: Bonding and Antibonding
Previous: Bonding and Antibonding
Contents
Index
We require the matrices
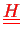 and
and
 ,
,
We have to solve
This give the eigenvalues of the energy,
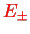 . We find the eigenvectors
. We find the eigenvectors
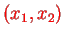 from
from
The normalisation constant is determined from
Summarising, we therefore have obtained the two molecular orbitals (MOs) with energies
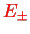 ,
,
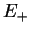 |
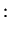 |
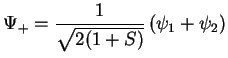 bonding bonding |
(3.18) |
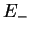 |
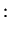 |
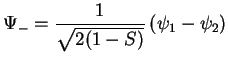 antibonding antibonding |
(3.19) |
Note that the normalisation factor is different for the two MOs, this is due to the fact that the original AOs (atomic orbitals) are not orthogonal.





Next: Explicit Calculation of ,
Up: Bonding and Antibonding
Previous: Bonding and Antibonding
Contents
Index
Tobias Brandes
2005-04-26
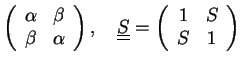
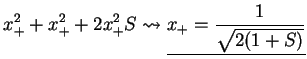
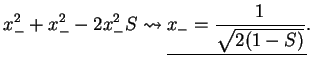
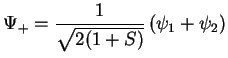 bonding
bonding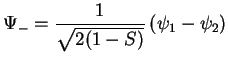 antibonding
antibonding