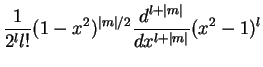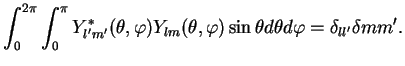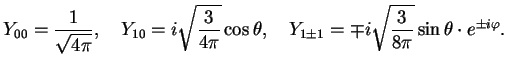Next: The Radial Part
Up: The Hydrogen Atom
Previous: Polar Coordinates
Contents
The angular part of (4.62) in fact is again an eigenvalue problem, because the equation
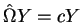 is an eigenvalue equation for the eigenvectors (eigenfunctions, remember
that a function is a vector in a Hilbert space) and possible eigenvalues
is an eigenvalue equation for the eigenvectors (eigenfunctions, remember
that a function is a vector in a Hilbert space) and possible eigenvalues 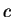 of the operator
of the operator
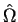 . Let us write down again this equation:
. Let us write down again this equation:
![$\displaystyle \left[\frac{1}{\sin \theta}\frac{\partial}{\partial \theta}
\left...
...\partial^2 Y(\theta,\varphi)}{\partial \varphi^2}\right]
= c Y(\theta,\varphi).$](img1217.png) |
|
|
(286) |
We do not explicitely construct the eigenfunctions 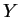 of the operator
of the operator
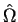 here but only give the results. In fact, this operator is
closely related to the angular momentum operator which we will discuss in the next session.
Similar to what we have found for the harmonic oscillator, it turns out
that solutions of (4.63) are possible only for
here but only give the results. In fact, this operator is
closely related to the angular momentum operator which we will discuss in the next session.
Similar to what we have found for the harmonic oscillator, it turns out
that solutions of (4.63) are possible only for 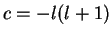 , where
, where
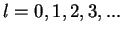 is an integer. All the solutions can be labeled by two quantum numbers
is an integer. All the solutions can be labeled by two quantum numbers
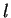 and
and 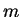 , where
, where 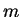 is an integer that can take the values
is an integer that can take the values
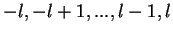 .
The solutions are called spherical harmonics and have the explicit form
.
The solutions are called spherical harmonics and have the explicit form
The 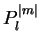 are called associated Legendre polynomials. The spherical harmonics
are an orthonormal function system on the surface of the unit sphere
are called associated Legendre polynomials. The spherical harmonics
are an orthonormal function system on the surface of the unit sphere
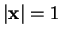 . We write
the orthonormality relation both in our abstract bra -ket and in explicit form:
. We write
the orthonormality relation both in our abstract bra -ket and in explicit form:
The spherical harmonics with
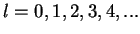 are denoted as
are denoted as
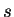 -,
-, 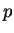 -,
-, 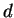 -,
-, 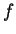 -,
-, 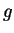 -,... functions which you might know already from chemistry (`orbitals').
The explicit forms for some of the first sphericals are
-,... functions which you might know already from chemistry (`orbitals').
The explicit forms for some of the first sphericals are
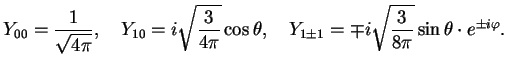 |
|
|
(289) |




Next: The Radial Part
Up: The Hydrogen Atom
Previous: Polar Coordinates
Contents
Tobias Brandes
2004-02-04
![$\displaystyle \left[\frac{1}{\sin \theta}\frac{\partial}{\partial \theta}
\left...
...\partial^2 Y(\theta,\varphi)}{\partial \varphi^2}\right]
= c Y(\theta,\varphi).$](img1217.png)
![$\displaystyle (-1)^{(m+\vert m\vert)/2}i^l
\left[\frac{2l+1}{4\pi}\frac{(l-\ver...
...}{(l+\vert m\vert)!}\right]^{1/2}
P_l^{\vert m\vert}(\cos \theta) e^{im\varphi}$](img1224.png)