




Next: Perturbation Theory in the
Up: Master Equation I: Derivation
Previous: Master Equation I: Derivation
Contents
Index
We define an interaction picture
by writing
 |
|
|
(4) |
with the Hamiltonian  describing the time evolution
of the uncoupled system and bath, and the perturbation
describing the time evolution
of the uncoupled system and bath, and the perturbation 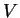 describing the interaction
describing the interaction 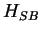 .
.
We define  as the total density matrix (system + bath) which obeys the
Liouville-von-Neumann equation ,
as the total density matrix (system + bath) which obeys the
Liouville-von-Neumann equation ,
![$\displaystyle \frac{d}{dt}\chi(t)=-i[H,\chi(t)] \leadsto \chi(t)= e^{-iHt} \chi(t=0) e^{iHt},$](img39.png) |
|
|
(5) |
where we start with the initial condition  at time
at time  .
In the interaction picture,
.
In the interaction picture,
The equation of motion for the density operator in the interaction picture becomes
In integral form, this can be written as
which we insert into Eq. (7.8) to obtain
![$\displaystyle \fbox{$ \begin{array}{rcl} \displaystyle
\frac{d}{dt} \tilde{\chi...
...]
-\int_0^t dt'[\tilde{V}(t),[\tilde{V}(t'),\tilde{\chi}(t')]].
\end{array}$\ }$](img55.png) |
|
|
(10) |
Up to here, everything is still exact.





Next: Perturbation Theory in the
Up: Master Equation I: Derivation
Previous: Master Equation I: Derivation
Contents
Index
Tobias Brandes
2004-02-18
![]() as the total density matrix (system + bath) which obeys the
Liouville-von-Neumann equation ,
as the total density matrix (system + bath) which obeys the
Liouville-von-Neumann equation ,
![$\displaystyle \frac{d}{dt}\chi(t)=-i[H,\chi(t)] \leadsto \chi(t)= e^{-iHt} \chi(t=0) e^{iHt},$](img39.png)