




Next: Single Path Integrals
Up: Feynman-Vernon Influence Functional Theories
Previous: Feynman-Vernon Influence Functional Theories
Contents
Index
This is a technique to solve the Liouville-von-Neumann Equation,
![$\displaystyle \frac{d}{dt}\chi(t)=-i[H,\chi(t)],\leadsto \chi(t)= e^{-iHt} \chi(t=0) e^{iHt},$](img674.png) |
|
|
(151) |
for the time-dependent density matrix  of system-bath Hamiltonians
of system-bath Hamiltonians
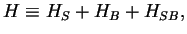 |
|
|
(152) |
cf. Eq. (7.4).
It is mainly useful for cases where the system Hamiltonian  referees to a single (or a few) degrees of
freedom, coupled via
referees to a single (or a few) degrees of
freedom, coupled via 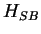 to a bath
to a bath  of many degrees of freedom.
The technique is based on double path integrals. The original
reference is R. P. Feynman, F. L. Vernon, Ann. Phys. (N. Y.) 24, 118 (1963).
of many degrees of freedom.
The technique is based on double path integrals. The original
reference is R. P. Feynman, F. L. Vernon, Ann. Phys. (N. Y.) 24, 118 (1963).
One of the applications of influence functional theories is the systematic derivation of a semiclassical
dynamics (Fokker-Planck equations, ...) from an exact quantum-mechanical theory:





Next: Single Path Integrals
Up: Feynman-Vernon Influence Functional Theories
Previous: Feynman-Vernon Influence Functional Theories
Contents
Index
Tobias Brandes
2004-02-18
![$\displaystyle \frac{d}{dt}\chi(t)=-i[H,\chi(t)],\leadsto \chi(t)= e^{-iHt} \chi(t=0) e^{iHt},$](img674.png)
![$\displaystyle \frac{d}{dt}\chi(t)=-i[H,\chi(t)],\leadsto \chi(t)= e^{-iHt} \chi(t=0) e^{iHt},$](img674.png)
![\includegraphics[width=0.5\textwidth]{semiclassics.eps}](img677.png)