




Next: Overview
Up: Origin of Dissipation, System-Bath
Previous: Example
Contents
Index
The basic idea in microscopic theories of dissipation is a decomposition
of a total system into a system  and a reservoir part
and a reservoir part  or
or 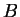 , `bath'.
The (Hamiltonian) dynamics of the total system
is reversible, but the dynamics of the system
, `bath'.
The (Hamiltonian) dynamics of the total system
is reversible, but the dynamics of the system  is effectively not
reversible for times
is effectively not
reversible for times  .
.
In this lecture, we formulate these ideas for quantum systems.
The Hilbert space of the total system is defined by the tensor product
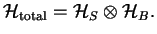 |
|
|
(2) |
The Hamiltonian of the total system is defined as
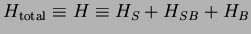 |
|
|
(3) |
Here and in the following, we will mostly discuss time-independent Hamiltonians.
Time-dependent Hamiltonians  can be treated as well but require
additional techniques (e.g., Floquet theory for period time-dependence; adiabatic
theorems for slow time-dependence).
can be treated as well but require
additional techniques (e.g., Floquet theory for period time-dependence; adiabatic
theorems for slow time-dependence).





Next: Overview
Up: Origin of Dissipation, System-Bath
Previous: Example
Contents
Index
Tobias Brandes
2004-02-18