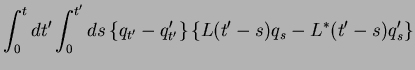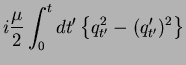Next: Propagator for Damped Harmonic
Up: Applications: Linear Coupling, Damped
Previous: Applications: Linear Coupling, Damped
Contents
Index
In many applications, one assumes (often for simplicity) a linear coupling to the bath,
![$\displaystyle H_B[x]+H_{SB}[xq]$](img894.png) |
 |
![$\displaystyle \sum_{\alpha=1}^N \left[
\frac{p_\alpha^2}{2M_\alpha}+ \frac{1}{2...
...ha^2 \left(x_\alpha -
\frac{c_\alpha}{M_\alpha\Omega_\alpha^2}q\right)^2\right]$](img895.png) |
|
| |
 |
![$\displaystyle \sum_{\alpha=1}^N \left[
\frac{p_\alpha^2}{2M_\alpha}+ \frac{1}{2...
...pha q x_\alpha
+\frac{1}{2}\frac{c_\alpha^2}{M_\alpha\Omega_\alpha^2}q^2\right]$](img896.png) |
|
![$\displaystyle {\cal F}[q_{t'},q'_{t'}]$](img821.png) |
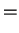 |
![$\displaystyle \exp \left\{-\Phi[q_{t'},q'_{t'}] \right\}$](img822.png) Influence Functional Influence Functional |
|
![$\displaystyle \Phi[q_{t'},q'_{t'}]$](img823.png) |
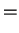 |
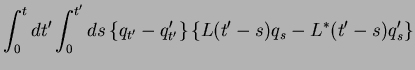 |
|
| |
 |
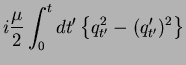 |
(208) |
Here, the kernel 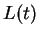 and the spectral density
and the spectral density  are
are
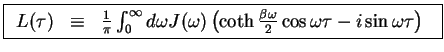 |
|
|
|
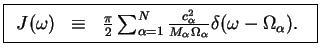 |
|
|
(209) |
Note that in this form, an additional term appears in 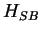 as a potential
as a potential
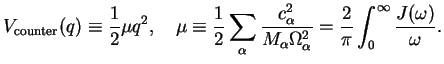 |
|
|
(210) |
Since the action  appears as
appears as
![$ \exp(iS[q])$](img903.png) in the path integral for
in the path integral for  and
and
![$ \exp(-iS[q])$](img904.png) in the path integral for
in the path integral for  , we could absorb the counter term into
the influence phase as
Note that the entire information on the coupling to the bath is now
contained in the spectral density
, we could absorb the counter term into
the influence phase as
Note that the entire information on the coupling to the bath is now
contained in the spectral density  , which we have defined following the
notation of Weiss, `Quantum Dissipative Systems'.
, which we have defined following the
notation of Weiss, `Quantum Dissipative Systems'.





Next: Propagator for Damped Harmonic
Up: Applications: Linear Coupling, Damped
Previous: Applications: Linear Coupling, Damped
Contents
Index
Tobias Brandes
2004-02-18
![$\displaystyle \sum_{\alpha=1}^N \left[
\frac{p_\alpha^2}{2M_\alpha}+ \frac{1}{2...
...ha^2 \left(x_\alpha -
\frac{c_\alpha}{M_\alpha\Omega_\alpha^2}q\right)^2\right]$](img895.png)
![$\displaystyle \sum_{\alpha=1}^N \left[
\frac{p_\alpha^2}{2M_\alpha}+ \frac{1}{2...
...pha q x_\alpha
+\frac{1}{2}\frac{c_\alpha^2}{M_\alpha\Omega_\alpha^2}q^2\right]$](img896.png)