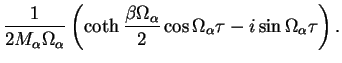Next: Linear Coupling
Up: Feynman-Vernon Influence Functional Theories
Previous: Linear Response, Fluctuation-Dissipation Theorem
Contents
Index
Our result for the influence phase can immediately be generalised to a single particle,
coupled to a system of  harmonic oscillators in thermal equilibrium,
harmonic oscillators in thermal equilibrium,
 |
 |
![$\displaystyle H_S[q] + H_B[x] + H_{SB}[xq]= H_S[q] + \sum_{\alpha=1}^N
\frac{p_\alpha^2}{2M_\alpha}+ \frac{1}{2}M_\alpha\Omega_\alpha x^2 +
f_\alpha[q] x_\alpha$](img890.png) |
|
![$\displaystyle {\cal F}[q_{t'},q'_{t'}]$](img821.png) |
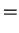 |
![$\displaystyle \exp \left\{-\Phi[q_{t'},q'_{t'}] \right\}$](img822.png) Influence Functional Influence Functional |
|
![$\displaystyle \Phi[q_{t'},q'_{t'}]$](img823.png) |
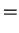 |
![$\displaystyle \sum_{\alpha=1}^N\int_{0}^{t}dt'\int_{0}^{t'}ds \left\{
f_\alpha[...
...ft\{ S_\alpha(t'-s) f_\alpha[q_{s}] - S_\alpha^*(t'-s) f_\alpha[q'_{s}]\right\}$](img891.png) |
|
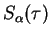 |
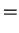 |
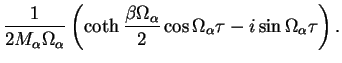 |
(207) |
Subsections
Tobias Brandes
2004-02-18
![$\displaystyle H_S[q] + H_B[x] + H_{SB}[xq]= H_S[q] + \sum_{\alpha=1}^N
\frac{p_\alpha^2}{2M_\alpha}+ \frac{1}{2}M_\alpha\Omega_\alpha x^2 +
f_\alpha[q] x_\alpha$](img890.png)
![$\displaystyle \sum_{\alpha=1}^N\int_{0}^{t}dt'\int_{0}^{t'}ds \left\{
f_\alpha[...
...ft\{ S_\alpha(t'-s) f_\alpha[q_{s}] - S_\alpha^*(t'-s) f_\alpha[q'_{s}]\right\}$](img891.png)
![$\displaystyle H_S[q] + H_B[x] + H_{SB}[xq]= H_S[q] + \sum_{\alpha=1}^N
\frac{p_\alpha^2}{2M_\alpha}+ \frac{1}{2}M_\alpha\Omega_\alpha x^2 +
f_\alpha[q] x_\alpha$](img890.png)
![$\displaystyle \sum_{\alpha=1}^N\int_{0}^{t}dt'\int_{0}^{t'}ds \left\{
f_\alpha[...
...ft\{ S_\alpha(t'-s) f_\alpha[q_{s}] - S_\alpha^*(t'-s) f_\alpha[q'_{s}]\right\}$](img891.png)