




Next: `Re-Exponentiation'
Up: Feynman-Vernon Influence Functional Theories
Previous: Propagator for Damped Harmonic
Contents
Index
(This sub-section is partly due to private communications from W. Zwerger).
Feynman and Vernon realised that the coupling of a system  to any bath
to any bath  can be mapped
onto the coupling to an equivalent oscillator bath, if the coupling is weak and second order perturbation
theory can be applied: let us have another look at
the operator form of the influence functional, Eq. (7.174),
can be mapped
onto the coupling to an equivalent oscillator bath, if the coupling is weak and second order perturbation
theory can be applied: let us have another look at
the operator form of the influence functional, Eq. (7.174),
where ![$ U_B[q]$](img745.png) is the time-evolution operator for
is the time-evolution operator for  and
and
![$ U_B^{\dagger}[q']$](img911.png) the (backwards in time) evolution operator for
the (backwards in time) evolution operator for  . Here,
. Here,  and
and
 refer to different paths
refer to different paths  and
and  .
.
Example: For a Fermi bath, we could have
![$\displaystyle H_0= \sum_k \varepsilon_k c^{\dagger}_k c_k,\quad V(t)\equiv V[q_t] =
\sum_{kk'} M_{kk'} \exp ({i(k-k')q_{t}}) c^{\dagger}_{k'} c_k.$](img913.png) |
|
|
(212) |
where
 creates a Fermion with quantum number
creates a Fermion with quantum number  .
.
We again introduce the interaction picture and write
The product of the two time-evolution operators therefore becomes
In order to be a little bit more definite, a useful parametrisation of the interaction operators might be
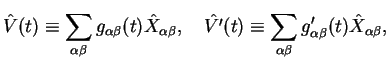 |
|
|
(215) |
with bath operators
 .
Note that this comprises the cases considered so far (harmonic oscillator, Fermi bath).
Taking the trace over
.
Note that this comprises the cases considered so far (harmonic oscillator, Fermi bath).
Taking the trace over  , we obtain
, we obtain
Introducing the correlation tensor
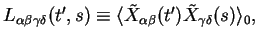 |
|
|
(217) |
this can be written as
Subsections





Next: `Re-Exponentiation'
Up: Feynman-Vernon Influence Functional Theories
Previous: Propagator for Damped Harmonic
Contents
Index
Tobias Brandes
2004-02-18
![$\displaystyle {\rm Tr_B} \left(\rho_B U_B^{\dagger}[q'] U_B[q] \right)$](img907.png)
![$\displaystyle {\rm Tr_B} \left(\rho_B U_B^{\dagger}[q'] U_B[q] \right)$](img907.png)
![$\displaystyle H_0= \sum_k \varepsilon_k c^{\dagger}_k c_k,\quad V(t)\equiv V[q_t] =
\sum_{kk'} M_{kk'} \exp ({i(k-k')q_{t}}) c^{\dagger}_{k'} c_k.$](img913.png)








![$\displaystyle 1 - i \int_{0}^{t}dt' \left\{ \tilde{V'}(t') - \tilde{V}(t') \rig...
...'}dt'ds \left\{\left[ \tilde{V'}(t')-\tilde{V}(t')\right] \tilde{V}(s) \right\}$](img924.png)
![$\displaystyle \int_{0}^{t}\int_{0}^{t'}dt'ds \left\{\tilde{V'}(s)
\left[ \tilde{V'}(t') - \tilde{V}(t')\right]\right\}+...$](img925.png)
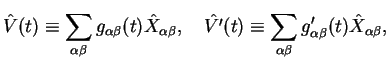
![$\displaystyle {\rm Tr_B} \left(\rho_B U_B^{\dagger}[q'] U_B[q] \right)\equiv
\langle U_B^{\dagger}[q'] U_B[q] \rangle_0$](img928.png)


![$\displaystyle g'_{\gamma\delta}(s) \langle \tilde{X}_{\gamma\delta}(s) \tilde{X}_{\alpha\beta}(t') \rangle_0
\Big]
+...$](img931.png)
![$\displaystyle {\cal F}[q(t'),q'(t')] = 1 - i\sum_{\alpha\beta} \int_{0}^{t}dt' ...
...}(t')-g_{\alpha\beta}(t')\right\}
\langle \tilde{X}_{\alpha\beta}(t') \rangle_0$](img933.png)
![$\displaystyle \sum_{\alpha\beta\gamma\delta}
\int_{0}^{t}\int_{0}^{t'}dt'ds \le...
...amma\delta}(t',s) - g'_{\gamma\delta}(s)
L_{\gamma\delta\alpha\beta}(s,t')\Big]$](img934.png)