`Re-Exponentiation'

So far this expression for the influence functional is very general, but it is only to second order in the system-bath interaction! In principle, one should write down the entire Dyson series for $U^{\dagger}_B[q']$ and $U_B[q]$ and sum up all the terms of the resulting expression in order to obtain the final result for the influence functional. Clearly, this is in general not possible, and it is even not guaranteed that such an expression would be convergent and mathematically meaningful.

For simplicity, let us assume that the linear term vanishes,

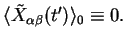$$\langle \tilde{X}_{\alpha\beta}(t') \rangle_0 \equiv 0.$$ (219)

For example, this is fullfilled for coupling to a linear harmonic oscillator, $\hat{X}_{\alpha\beta} \equiv \delta_{\alpha\beta} \hat{x}$ with $\hat{x}$ the oscillator coordinate.

At least some contributions to the infinite series for ${\cal F}[q(t'),q'(t')]$ can be summed up in closed form: this is done by `re-exponentiation'. In fact, up to second order in the system-bath interaction, we can write (summarising all our definitions so far)

$$\hat{V}[q_{t}] \equiv \sum_{\alpha\beta}g_{\alpha\beta}[q_{t}] \hat{X}_{\alpha\beta}, \... ...\equiv \langle \tilde{X}_{\alpha\beta}(t') \tilde{X}_{\gamma\delta}(s)\rangle_0$$

$${\cal F}^{\rm pert}[q(t'),q'(t')] = \exp \{- \Phi^{\rm pert} [q(t'),q'(t')]\},$$

$$\Phi^{\rm pert} [q(t'),q'(t')] = \sum_{\alpha\beta\gamma\delta} \int_{0}^{t}\int_{0}^{t'}dt'ds \left\{ g_{\alpha\beta}[q_{t'}]-g_{\alpha\beta}[q'_{t'}]\right\}$$

$$\times \Big[ g_{\gamma\delta}[q_s] L_{\alpha\beta\gamma\delta}(t',s) - g_{\gamma\delta}[q'_s] L_{\gamma\delta\alpha\beta}(s,t')\Big]$$ (220)

by simply expanding the exponential. The `re-exponentiation' automatically sums up an infinite number of terms. Such `exponentiation' schemes are known, e.g., from cluster expansions of the statistical operator $e^{-\beta \hat{H}}$. The important observation here is that for the harmonic oscillator case, this re-exponentiation becomes exact: with $\hat{V}=f[q]\hat{x}$ and $\hat{V'}=f[q']\hat{x}$, we recognise

$$\Phi [q(t'),q'(t')] = \int_{0}^{t}\int_{0}^{t'}dt'ds \left\{ f[q_{t'}] - f[q'_{t'}] \right\} \left\{ L(t',s) f[q_{s}] - L(s,t') f[q'_{s}]\right\},$$ (221)

$$L(t',s) = \langle x(t') x(s) \rangle_0 = \langle x(t'-s) x \rangle_0=L(t'-s)$$

$$L(s,t') = \langle x(s) x(t') \rangle_0 = \langle x(t') x(s) \rangle_0^* = L^*(t'-s),$$ (222)

and therefore by comparison with Eq. (7.189) we find that both expressions co-incide.