`Semiclassical' Limit for Damped Single Particle Motion

References: A. Schmid, J. Low Temp. Phys. 49, 609 (1982); W. Zwerger, Phys. Rev. B 35, 4737 (1987); N. Janssen and W. Zwerger, Phys. Rev. B 52, 9406 (1995); U. Weiss, `Quantum Dissipative Systems' (2nd ed.), World Scientific (Singapore) (1999), ch. 5.5.

Let us assume a single particle in a potential $V(q)$,

$$H_S = \frac{p^2}{2m}+V(q).$$ (223)

We consider the reduced density matrix $\rho(t)$ of the system $S$,

$$\rho(x,y,t)\equiv \langle x+y/2\vert \rho(t) \vert x-y/2\rangle,$$ (224)

where we set

$$q=x+y/2,\quad q'=x-y/2;\quad x = \frac{1}{2}\left(q+q'\right),\quad y=q-q',$$ (225)

thus introducing the `center-of-mass' coordinate 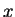$x$ and the relative coordinate $y$. Note that the Wigner distribution function $f(x,p,t)$ is obtained from the density matrix as a Fourier transform with respect to the relativ co-ordinate $y$,

$$f(x,p,t)=\int_{-\infty}^{\infty}\frac{dy}{2\pi}\rho(x,y,t)e^{-ipy}.$$ (226)

Correspondingly, in the double path integral we integrate over center-of-mass-coordinate and relative-coordinate paths,

$$x_t = \frac{1}{2}\left(q_t+q_t'\right),\quad y_t=q_t-q_t'$$ (227)

The Jacobian of the corresponding discretised variable transformation is one whence one can write

$$\rho(x,y,t) = \int dx_0 dy_0 \rho_0(x_0,y_0) J(x,y,t;x_0,y_0)$$

$$J(x,y,t;x_0,y_0) = \int_{x_0}^x {\cal D}x \int_{y_0}^y{\cal D}y \exp \left[ i\int_{0}^{t}dt'\left(M\dot{x}_{t'}\dot{y}_{t'} - V(x+y/2) + V(x-y/2) \right)\right]$$

$$\times \exp \left\{-\Phi[x_{t'},y_{t'}] \right\}$$ (228)