




Next: Wigner Distribution in `Semi-classical'
Up: `Semiclassical' Limit for Damped
Previous: Expansion of the Influence
Contents
Index
This is a useful trick when dealing with functional integrals.
We start from the identity for a real symmetric, positive definite  matrix
matrix 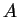 ,
,
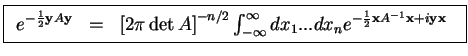 |
|
|
(236) |
Exercise: Prove this identity. Hint: use the standard formula for Gaussian integrals
and a linear transformation that diagonalises 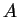 .
.
We now obtain
Here, we have used the fact that the discrete inverse of an operator needs to be divided
by
 ,
,
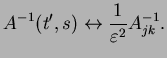 |
|
|
(238) |
This can be derived by considering the discrete equivalent of the delta function and
leads to the following translation table between continuous and discrete:
Now using the fact that  is symmetric in
is symmetric in 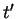 and
and  ,
we have
,
we have
![$\displaystyle \int_{0}^{t}dt'\int_{0}^{t'}ds \varphi_2[x_s] {{y_{t'}y_{s}}}=
\frac{1}{2}\int_{0}^{t}dt\int_{0}^{t}ds \varphi_2[x_s] {{y_{t'}y_{s}}}$](img1026.png) |
|
|
(240) |
and therefore
Here we have explicitly indicated the dependence of the measure
![$ {\cal D}\xi[x]$](img1031.png) on
the paths
on
the paths  , which enters through the determinant of the operator
, which enters through the determinant of the operator
![$ \varphi_2[x_s]$](img1033.png) .
The pathintegral over
.
The pathintegral over  is now very easy: we find (
is now very easy: we find (
 )
)
Here,  indicates the product of delta functions that fixes the
indicates the product of delta functions that fixes the  path to the
path to the
 path, and for
path, and for
 the
the
 becomes irrelevant.
Inserting yields
becomes irrelevant.
Inserting yields





Next: Wigner Distribution in `Semi-classical'
Up: `Semiclassical' Limit for Damped
Previous: Expansion of the Influence
Contents
Index
Tobias Brandes
2004-02-18
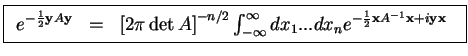
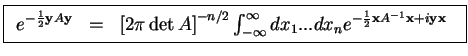
![]() .
.
![$\displaystyle \exp \left[-\frac{1}{2}\int_{0}^{t}\int_{0}^{t}dt'ds A(t',s) {{y_...
...y} \exp \left[-\frac{\varepsilon^2}{2} \sum_{j,k=0}^{N-1} A_{jk}y_j y_k \right]$](img1010.png)
![$\displaystyle \lim_{N\to \infty} \left[2\pi \det A \right]^{-N/2}
\int d\xi_0.....
...}_{jk}}{\varepsilon^2}
\xi_k + i \varepsilon\sum_{j=0}^{N-1} y_j \xi _j \right]$](img1011.png)
![$\displaystyle \int {\cal D}\xi \exp \left[- \int_{0}^{t}\int_{0}^{t}dt'ds \xi_{t'}A^{-1}(t',s)\xi_{s}
+ i \int_{0}^{t} dt' y_{t'} \xi_{t'} \right]$](img1012.png)
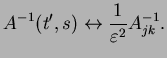





![$\displaystyle \int_{0}^{t}dt'\int_{0}^{t'}ds \varphi_2[x_s] {{y_{t'}y_{s}}}=
\frac{1}{2}\int_{0}^{t}dt\int_{0}^{t}ds \varphi_2[x_s] {{y_{t'}y_{s}}}$](img1026.png)

![$\displaystyle \exp \left[
-i\int_{0}^{t}dt' y_{t'}
\left\{ M\ddot{x}_{t'} + V'(...
...frac{1}{2}\int_{0}^{t}\int_{0}^{t}dt' ds \varphi_2[x_s] {{y_{t'}y_{s}}}
\right]$](img1028.png)
![$\displaystyle \int_{x_0}^x {\cal D}x \int_{y_0}^y{\cal D}y e^{iM( \dot{x}_{t}y
...
...{1}{2}
\int_{0}^{t}\int_{0}^{t}dt'ds \xi_{t'}\varphi_2[x_s]^{-1}\xi_{s} \right]$](img1029.png)
![$\displaystyle \exp \left[
-i\int_{0}^{t}dt' y_{t'}
\left\{ M\ddot{x}_{t'} + V'(x_{t'}) + F_B[x_s,t'] -\xi_{t'} \right\}
\right].$](img1030.png)
![$\displaystyle \int_{y_0}^y{\cal D}y
\exp \left[ -i\int_{0}^{t}dt' y_{t'} b_{t'}...
...}\right)^\frac{N}{2}
\exp \left[ -{i\varepsilon}\sum_{j=0}^{N-1} y_jb_j \right]$](img1036.png)

![$\displaystyle J_{\rm sc}(x,y,t;x_0,y_0) = e^{iM( \dot{x}_{t}y- \dot{x}_{0}y_0)}...
...{1}{2}
\int_{0}^{t}\int_{0}^{t}dt'ds \xi_{t'}\varphi_2[x_s]^{-1}\xi_{s} \right]$](img1041.png)