Wigner Distribution in `Semi-classical' Limit

Considering now the definition of the Wigner distribution function,

$$f_{\rm sc}(x,p,t) = \int_{-\infty}^{\infty}\frac{dy}{2\pi}\rho(x,... ...\frac{dy}{2\pi}e^{-ipy} \int dx_0dy_0 \rho_0(x_0,y_0) J_{\rm sc}(x,y,t;x_0,y_0)$$

$$= \int \frac{dy}{2\pi} dx_0dy_0 \rho_0(x_0,y_0) e^{-ipy}e^{iM( \dot... ... \frac{1}{2} \int_{0}^{t}\int_{0}^{t}dt'ds \xi_{t'}\varphi_2[x_s]^{-1}\xi_{s} }$$

$$\times \Delta( M\ddot{x}_{t'} + V'(x_{t'}) + F_B[x_s,t'] -\xi_{t'} )$$

$$= \int dx_0 f_0(x_0,p_0=M\dot{x_0}) \delta(p-M\dot{x}) \int_{x_0}^x... ... \frac{1}{2} \int_{0}^{t}\int_{0}^{t}dt'ds \xi_{t'}\varphi_2[x_s]^{-1}\xi_{s} }$$

$$\times \Delta( M\ddot{x}_{t'} + V'(x_{t'}) + F_B[x_s,t'] -\xi_{t'} ).$$ (244)

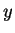Here, the $y$-integral generated $\delta(p-M\dot{x})$, and the $y_0$-integral transformed the initial condition $\rho_0(x_0,y_0)$ into its Wigner transform $f_0(x_0,p_0=M\dot{x_0})$. We summarise,

$$\fbox{$ \begin{array}{rcl} \displaystyle & & f_{\rm sc}(x,p,t) = ... ... \Delta( M\ddot{x}_{t'} + V'(x_{t'}) + F_B[x_s,t'] -\xi_{t'} ). \end{array}$\ }$$ (245)