Discussion

In the semi-classical approximation, the time-evolution of the Wigner-distribution function is determined by Eq. (7.249). This equation describes a stochastic process for the center-of-mass co-ordinate $x_{t'}$ of the particle, moving within a potential $V(x)$ under the action of a deterministic friction force $F_B[x_s,t']$,

$$F_B[x_s,t'] = -\sum_{\alpha=1}^N \int_{0}^{t'}ds \frac{\sin \Omega_\alpha (t'-s)} {M_\alpha\Omega_\alpha} f'_\alpha[x_{t'}]f_\alpha[x_{s}],$$ (246)

and a stochastic force $\xi_{t'}$. The motion of the particle is governed by the stochastic integro-differential equation

$$M\ddot{x}_{t'} + V'(x_{t'}) + F_B[x_s,t'] =\xi_{t'},$$ (247)

where the stochastic force $\xi_{t'}$ is a random force which itself depends on the coordinate of the particle: this can be seen by the fact that its variance,

$$\langle \xi_{t'} \xi_{s} \rangle = \varphi_2[x]= \sum_{\alpha=1}^... ...a\Omega_\alpha}{2} \cos \Omega_\alpha (t'-s) f'_\alpha[x_{t'}]f'_\alpha[x_{s}],$$ (248)

depends on the particle path $x_s$. The Wigner distribution is obtained by integrating over all possible realisations of the stochastic force, such that Eq. (7.252) is fulfilled. Since the ${\cal}\xi$ path-integral is Gaussian, one speaks of a Gaussian stochastic process. This of course is due to the fact that we truncated the $y_{t'}$ expansion in the influence phase after the term quadratic in $y_{t'}$.

Our results shows that the influence of the bath is two-fold: it leads to a deterministic, retarded `friction' force, and to a stochastic force. The latter contains the temperature and, by means of the $\coth (\beta \hbar \Omega/2)$ terms in $\varphi_2[x]$, a fully quantum mechanical description of the bath.

For certain types of system-bath couplings, one can explicitely show that the operator $\varphi_2$ is positive definite and therefore, the term quadratic in $y_{t'}$ in the original double path integral exponentially suppresses strong deviations from the diagonal paths with $y_{t'} =0$. In this case, the expansion of the one-particle potential $V$,

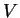$$-V(x+y/2) + V(x-y/2) \approx -V'(x) y$$ (249)

becomes more plausible. One should, however, expect that quantum mechanical effects (like particle tunneling) are destroyed by the approximation Eq. (7.253).