




Next: Completing the Square
Up: `Semiclassical' Limit for Damped
Previous: `Semiclassical' Limit for Damped
Contents
Index
Expansion of the Influence Phase
In order to derive a semiclassical limit from the double path integral, the
central idea is to expand the influence phase in powers of the
paths  . The
. The  -paths describe `off-diagonal excursions' from the diagonal
paths
-paths describe `off-diagonal excursions' from the diagonal
paths  in the time-evolution of
in the time-evolution of  . We write
. We write
![$\displaystyle {\cal F}[x_{t'},y_{t'}]$](img970.png) |
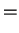 |
![$\displaystyle \exp \left\{-\Phi[x_{t'},y_{t'}] \right\}$](img967.png) Influence Functional Influence Functional |
|
![$\displaystyle -\Phi[x_{t'},y_{t'}]$](img971.png) |
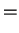 |
![$\displaystyle -\sum_{\alpha=1}^N\int_{0}^{t}dt'\int_{0}^{t'}ds \left\{
f_\alpha[x_{t'}+y_{t'}/2] - f_\alpha[x_{t'}-y_{t'}/2] \right\}$](img972.png) |
|
| |
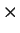 |
![$\displaystyle \left\{ S_\alpha(t'-s) f_\alpha[x_{s}+y_{s}/2] - S_\alpha^*(t'-s) f_\alpha[x_{s}-y_{s}/2]\right\}$](img973.png) |
|
| |
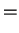 |
![$\displaystyle -\sum_{\alpha=1}^N\int_{0}^{t}dt'\int_{0}^{t'}ds
f'_\alpha[x_{t'}]y_{t'}$](img974.png) |
|
| |
 |
![$\displaystyle \left\{\mbox{\rm Re } S_\alpha(t'-s) f'_\alpha[x_{s}]y_{s} + 2i \mbox{\rm Im }
S_\alpha(t'-s) f_\alpha[x_{s}]\right\} + O\left[y_s\right]^3.$](img975.png) |
(229) |
In the semiclassical approximation, we thus can write the influence as
Exercise: Check that for the linear model (coupling linear in  ),
Eq.(7.212), the influence phase becomes
),
Eq.(7.212), the influence phase becomes
For the linear model, the semiclassical expansion of the influence phase is therefore exact.
In a similar way, we expand the potential
 in the action in powers of the off-diagonal path
in the action in powers of the off-diagonal path  , thus arriving at
, thus arriving at
The first step now is to perform an integration by parts to transform the term
 ,
and to re-arrange
,
and to re-arrange
This is an interesting expression: the term in the brackets  looks likely to lead
to a classical equation of motion,
looks likely to lead
to a classical equation of motion,
![$\displaystyle M\ddot{x}_{t'} + V'(x_{t'}) + F_B[x_s,t'] =0,$](img1000.png) |
|
|
(234) |
where
 is the force due to the potential
is the force due to the potential  , and
, and
![$ F_B[x_s,t']$](img1002.png) is a retarded, position-dependent deterministic friction force due to the
bath. In addition, however, there is the term quadratic in
is a retarded, position-dependent deterministic friction force due to the
bath. In addition, however, there is the term quadratic in  containing
the function
containing
the function
which is the only place where the bath temperature  enters.
enters.





Next: Completing the Square
Up: `Semiclassical' Limit for Damped
Previous: `Semiclassical' Limit for Damped
Contents
Index
Tobias Brandes
2004-02-18
![$\displaystyle -\sum_{\alpha=1}^N\int_{0}^{t}dt'\int_{0}^{t'}ds \left\{
f_\alpha[x_{t'}+y_{t'}/2] - f_\alpha[x_{t'}-y_{t'}/2] \right\}$](img972.png)
![$\displaystyle -\sum_{\alpha=1}^N\int_{0}^{t}dt'\int_{0}^{t'}ds
f'_\alpha[x_{t'}]y_{t'}$](img974.png)
![$\displaystyle -\sum_{\alpha=1}^N\int_{0}^{t}dt'\int_{0}^{t'}ds \left\{
f_\alpha[x_{t'}+y_{t'}/2] - f_\alpha[x_{t'}-y_{t'}/2] \right\}$](img972.png)
![$\displaystyle -\sum_{\alpha=1}^N\int_{0}^{t}dt'\int_{0}^{t'}ds
f'_\alpha[x_{t'}]y_{t'}$](img974.png)
![$\displaystyle -
i \int_{0}^{t}dt'\int_{0}^{t'}ds \varphi_1[x_s] \underline{\underline{y_{t'}}},\quad
\varphi_1[x_s]\equiv \sum_{\alpha=1}^N 2$](img979.png) Im
Im ![$\displaystyle \int_{0}^{t}dt'\int_{0}^{t'}ds \varphi_2[x_s] \underline{\underline{y_{t'}y_{s}}},\quad
\varphi_2[x_s]\equiv \sum_{\alpha=1}^N$](img982.png) Re
Re ![]() ),
Eq.(7.212), the influence phase becomes
),
Eq.(7.212), the influence phase becomes
![]() in the action in powers of the off-diagonal path
in the action in powers of the off-diagonal path ![]() , thus arriving at
, thus arriving at

![$\displaystyle \int_{x_0}^x {\cal D}x \int_{y_0}^y{\cal D}y \exp \left[
i\int_{0}^{t}dt'\left(M\dot{x}_{t'}\dot{y}_{t'} - V'(x_{t'})y_{t'} \right)\right]$](img991.png)
![$\displaystyle \exp \left\{
-i \int_{0}^{t}dt'\int_{0}^{t'}ds \varphi_1[x_s] {{y_{t'}}}
-\int_{0}^{t}dt'\int_{0}^{t'}ds \varphi_2[x_s] {{y_{t'}y_{s}}}
\right\}.$](img992.png)
![$\displaystyle J_{\rm sc}(x,y,t;x_0,y_0) = \int_{x_0}^x {\cal D}x \int_{y_0}^y{\cal D}y \exp \left[iM( \dot{x}_{t}y
- \dot{x}_{0}y_0)\right]$](img994.png)
![$\displaystyle \exp \left[
-i\int_{0}^{t}dt' y_{t'}
\left\{ M\ddot{x}_{t'} + V'(...
...\right\}
-\int_{0}^{t}dt'\int_{0}^{t'}ds \varphi_2[x_s] {{y_{t'}y_{s}}}
\right]$](img995.png)
![$\displaystyle \int_{0}^{t'}ds \varphi_1[x_s]
= \int_{0}^{t'}ds\sum_{\alpha=1}^N 2$](img997.png) Im
Im ![$\displaystyle -\sum_{\alpha=1}^N \int_{0}^{t'}ds
\frac{\sin \Omega_\alpha (t'-s)} {M_\alpha\Omega_\alpha} f'_\alpha[x_{t'}]f_\alpha[x_{s}].$](img998.png)