




Next: Linear Response, Fluctuation-Dissipation Theorem
Up: Influence Functional for Coupling
Previous: Time-evolution operator
Contents
Index
Influence Phase
The influence phase can be obtained directly from its definition, Eq. (7.173),
where for a moment we abbreviated 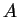 ,
,  etc. for the integrals Eq. (7.181) with
etc. for the integrals Eq. (7.181) with
 in the undashed and
in the undashed and
 in the dashed (not the derivative)
quantities.
We now assume a thermal equilibrium for the density operator
in the dashed (not the derivative)
quantities.
We now assume a thermal equilibrium for the density operator  ,
,
where we used the matrix elements of the propagator
 for
for
 (Wick rotation of the time
(Wick rotation of the time  ). Doing the Gaussian integral yields
). Doing the Gaussian integral yields
the last step now is to re-insert the definitions of
 . The resulting long expression
. The resulting long expression
can be further simplified with
![$ \sin \alpha\cos \beta = \frac{1}{2}[\sin (\alpha-\beta) + \sin ( \alpha+\beta)]$](img816.png) and carefully considering the limits of the integrals and the symmetry of the integrands.
Re-installing furthermore
and carefully considering the limits of the integrals and the symmetry of the integrands.
Re-installing furthermore
![$ g_{t'}\equiv g(t') \equiv f[q_{t'}]$](img817.png) (we write the time-arguments as an index
to avoid bulky expressions with too many brackets),
the result can be written in a compact form,
the Feynman-Vernon Influence Functional for the coupling of a single particle to a single harmonic oscillator
in thermal equilibrium,
(we write the time-arguments as an index
to avoid bulky expressions with too many brackets),
the result can be written in a compact form,
the Feynman-Vernon Influence Functional for the coupling of a single particle to a single harmonic oscillator
in thermal equilibrium,
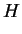 |
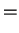 |
![$\displaystyle H_S[q] + H_B[x] + H_{SB}[xq]= H_S[q] + \frac{p^2}{2M}+ \frac{1}{2}M\Omega^2 x^2 + f[q] x$](img819.png) |
|
 |
 |
![$\displaystyle \int dq_0dq_0' \langle q_0 \vert\rho(0)\vert q_0'\rangle
\int_{q_...
...p\left[ i \left(S[q] - S[q']\right)\right] \underline{{\cal F}[q_{t'},q'_{t'}]}$](img820.png) |
|
![$\displaystyle {\cal F}[q_{t'},q'_{t'}]$](img821.png) |
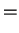 |
![$\displaystyle \exp \left\{-\Phi[q_{t'},q'_{t'}] \right\}$](img822.png) Influence Functional Influence Functional |
|
![$\displaystyle \Phi[q_{t'},q'_{t'}]$](img823.png) |
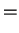 |
![$\displaystyle \int_{0}^{t}dt'\int_{0}^{t'}ds \left\{
f[q_{t'}] - f[q'_{t'}] \right\}
\left\{ L(t'-s) f[q_{s}] - L^*(t'-s) f[q'_{s}]\right\}$](img824.png) |
|
 |
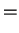 |
 |
(185) |





Next: Linear Response, Fluctuation-Dissipation Theorem
Up: Influence Functional for Coupling
Previous: Time-evolution operator
Contents
Index
Tobias Brandes
2004-02-18
![$\displaystyle {\rm Tr_B} \left(\rho_B U_B^{\dagger}[q'] U_B[q] \right)
= {\rm T...
... \left(\rho_B \tilde{U}^{\dagger}[q'] e^{iH_0t} e^{-iH_0t} \tilde{U}[q] \right)$](img791.png)



![$\displaystyle {\rm Tr_B} \left(\rho_B U_B^{\dagger}[q'] U_B[q] \right)
= {\rm T...
... \left(\rho_B \tilde{U}^{\dagger}[q'] e^{iH_0t} e^{-iH_0t} \tilde{U}[q] \right)$](img791.png)




![$\displaystyle \frac{1}{Z}\sqrt{\frac{M\Omega}{2\pi \sinh \Omega \beta}}
\exp \l...
... }
\left [ \left( x^2+x'^2\right) \cosh \beta \Omega - 2 x x' \right] \right\},$](img802.png)
![$\displaystyle {\cal F}[q(t'),q'(t')] = e^{i(A'-A)} \int dx \langle x\vert \rho_B \vert x +C-C' \rangle e^{i(B'-B)(x+C)}$](img805.png)

![$\displaystyle \exp \left\{ -\frac{M\Omega}{2 \sinh \beta \Omega }
\left [ \left( x^2+(x+C-C')^2\right) \cosh \beta \Omega - 2 x (x+C-C') \right] \right\}$](img807.png)
![$\displaystyle \left[\mbox{\rm use } \tanh \frac{x}{2}=\frac{\cosh x -1}{\sinh x},\quad
\coth x -\frac{1}{2}\tanh \frac{x}{2}=\frac{1}{2}\coth \frac{x}{2}\right]$](img808.png)

![$\displaystyle \exp \left\{ -\frac{1}{4M\Omega}
\coth\frac{\beta\omega}{2}\left[ (B'-B)^2 + M^2\Omega^2(C-C')^2\right] \right\}.$](img810.png)



