




Next: Influence Phase
Up: Influence Functional for Coupling
Previous: Influence Functional for Coupling
Contents
Index
This is given by the solution of the Schrödinger equation,
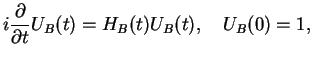 |
|
|
(172) |
the formal solution of which is
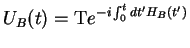 |
|
|
(173) |
with the time-ordering operator T. Now, 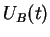 can't be directly calculated from
Eq. (7.177) because the
can't be directly calculated from
Eq. (7.177) because the 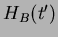 do not commute with each other at different times
do not commute with each other at different times
![[*]](file:/usr/share/latex2html/icons/footnote.png) .
One solution is to calculate
.
One solution is to calculate 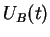 by direct evaluation of the path integral which is tedious but can be done.
Here, we show an alternative solution: introduce the interaction picture and write
by direct evaluation of the path integral which is tedious but can be done.
Here, we show an alternative solution: introduce the interaction picture and write
We solve for
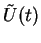 by making the general ansatz
by making the general ansatz
with functions 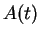 etc to be determined by taking the time-derivative of
etc to be determined by taking the time-derivative of
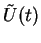 . This yields
. This yields
Therefore, comparing with the expression for
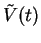 yields
yields
and therefore,
In order to get explicit results here, we now need the propagator matrix elements
for the harmonic oscillator,
![$\displaystyle \fbox{$ \displaystyle \langle x\vert e^{-iH_0 t}\vert x'\rangle =...
...a t}
\left [ \left( x^2+x'^2\right) \cos \Omega t - 2 x x' \right] \right\}. $}$](img784.png) |
|
|
(179) |
These again can either be obtained by direct evaluation of the single path integral for the harmonic oscillator
or (somewhat simpler) by using the stationary eigenstates. The matrix element
for the driven harmonic oscillator,
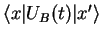 ,
can then after some transformations (straightforward algebra with trig functions)
be written as
,
can then after some transformations (straightforward algebra with trig functions)
be written as
This coincides with the result given in L. S. Schulman, Techniques and Applications of Path Integration,
Wiley (1981).





Next: Influence Phase
Up: Influence Functional for Coupling
Previous: Influence Functional for Coupling
Contents
Index
Tobias Brandes
2004-02-18
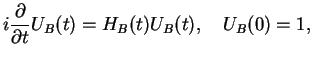
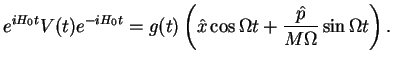
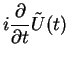
![$\displaystyle \dot{A}(t) \tilde{U}(t) + \hat{x} \dot{B}(t) \tilde{U}(t)
+ \dot{...
...B(t)\hat{x}} +\left[e^{-iB(t)\hat{x}},\hat{p}\right]}
\right) e^{-iC(t)\hat{p}}$](img772.png)
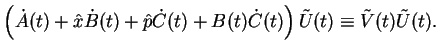
![$\displaystyle \fbox{$ \displaystyle \langle x\vert e^{-iH_0 t}\vert x'\rangle =...
...a t}
\left [ \left( x^2+x'^2\right) \cos \Omega t - 2 x x' \right] \right\}. $}$](img784.png)
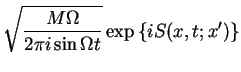
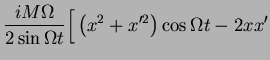
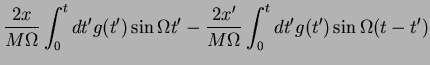
![$\displaystyle \frac{2}{M^2\Omega^2}\int_{0}^{t}\int_{0}^{t'}dt'ds g(t') g(s)\sin \Omega (t-t')\sin \Omega s \Big].$](img790.png)