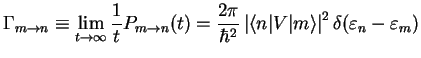Next: Higher Order Perturbation Theory
Up: First Order Perturbation Theory
Previous: First Order Perturbation Theory
Contents
Index
In this case
As for the
 function, we now use the representation of the Dirac Delta-function,
function, we now use the representation of the Dirac Delta-function,
Theorem:
For any integrable, normalised function
 with
with
 ,
,
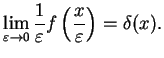 |
|
|
(3.12) |
Here, we apply it with

This is an extremely important result, and we therefore highlight it here again, introducing the
transition rate
 ,
,
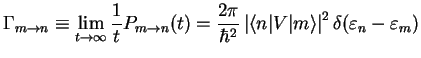 |
|
|
(3.14) |
The total transition rate into any final state
 is, within first order perturbationtheory in
is, within first order perturbationtheory in
 , given by the sum over all
, given by the sum over all
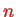 ,
,





Next: Higher Order Perturbation Theory
Up: First Order Perturbation Theory
Previous: First Order Perturbation Theory
Contents
Index
Tobias Brandes
2005-04-26



![]() with
with
![]() ,
,
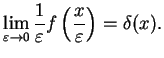
![]()



![$\displaystyle \lim_{t\to \infty } \left\vert\langle n\vert V\vert m\rangle \rig...
... \frac{\varepsilon_n-\varepsilon_m}{2} t}{[(\varepsilon_n-\varepsilon_m)t/2]^2}$](img1181.png)