




Next: Time-Independent Hamiltonian
Up: Time-Dependent Perturbation Theory
Previous: The Interaction Picture
Contents
Index
This is achieved by doing the first iteration in
We take
 for simplicity and the initial state therefore is
for simplicity and the initial state therefore is
 ,
,
This can be worked out in some more detail by assuming a basis
 of eigenstates of
of eigenstates of
 ,
,
Let us assume the initial state
 is an eigenstate of
is an eigenstate of
 , then
, then
The probability to find the system in state
 after time
after time
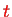 is then a transition probability.
Use
is then a transition probability.
Use
 (EXERCISE:CHECK!) to find within first order perturbation theory
(EXERCISE:CHECK!) to find within first order perturbation theory
Subsections





Next: Time-Independent Hamiltonian
Up: Time-Dependent Perturbation Theory
Previous: The Interaction Picture
Contents
Index
Tobias Brandes
2005-04-26










 first order
first order