Longitudinal $\mathbf{E}$ and $\mathbf{B}$ are `trivial'

For the magnetic field, one has

$$= \div\mathbf{B}\leadsto 0= {\bf k}\cdot \hat{\mathbf{B}}({\bf k}) \leadsto \hat{\mathbf{B}}_\Vert({\bf k}) =0 \leadsto \mathbf{B}_\Vert=0,$$ 0 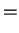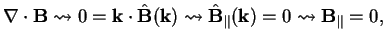(1.9)

which means that the magnetic field is purely transversal, i.e. $\mathbf{B}= \mathbf{B}_\perp$.

For the electric field, one has

$$\varepsilon_0 \div\mathbf{E} = \rho,\quad \varepsilon_0 i {\bf k} \cdot \hat{\mathbf{E}}({\bf k}... ...thbf{E}}_\Vert({\bf k},t) = -\frac{i{\bf k}}{\varepsilon_0k^2} \rho({\bf k},t),$$ (1.10)

at all times $t$ the longitudinal electric field is determined by the charge distribution at the same time (no retardation effects).

Therefore, the longitudinal fields are no independent variables; they are either zero for the magnetic field ( $\mathbf{B}_\Vert=0$) or just given by the charge in the case of the electric field. By contrast, the transverse fields are independent variables.