Potentials

The Maxwell equations are a system of first order PDEs that can be transformed into second order equations by introduction of potentials.

• This facilitates quantization of the em field by the analogy with harmonic oscillators in Newtons equations.
• This also is in analogy with classical mechanics, where one tries to work with potentials instead of forces which often simplifies things.

One has

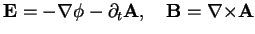$$\mathbf{E}= -\nabla \phi - \partial_t \mathbf{A},\quad \mathbf{B}= \mathbf{\nabla \times} \mathbf{A}$$ (1.11)

with the scalar potential $\phi$ and the vector potential $\mathbf{A}$. In Fourier space,

$$\hat{\mathbf{E}}({\bf k}) = -i {\bf k}\phi({\bf k}) - \partial_t\hat{\mathbf{A}}({\bf k})\leadsto \hat{\mathbf{E}}_\perp({\bf k})= - \partial_t\hat{\mathbf{A}}_\perp({\bf k})$$ (1.12)

$$\hat{\mathbf{B}}({\bf k}) = i {\bf k}\times \hat{\mathbf{A}}({\bf k})= i{\bf k}\times \hat{\mathbf{A}}_\perp({\bf k}).$$ (1.13)

The`non-trivial' transverse components of the field are therefore determined only by the transverse component $\hat{\mathbf{A}}_\perp$ of the vector potential.