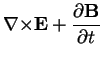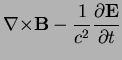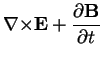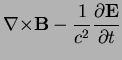Next: Longitudinal and transversal parts Up: Interaction with Light Previous: Interaction with Light Contents Index

Electromagnetic Fields and Maxwells Equations

Literature here: R. Loudon `The Quantum Theory of Light' [6] and C. Cohen-Tannoudji, J. Dupont-Roc, G. Grynberg `Atom-Photon Interactions' [7].

Electromagnetism brings in the notion of fields as described by Maxwell's equations

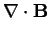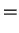$\displaystyle \div\mathbf{B}$	$\displaystyle =$	0	(1.1)
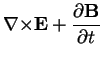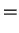$\displaystyle \mathbf{\nabla \times} \mathbf{E}+ \frac{\partial \mathbf{B}}{\partial t}$	$\displaystyle =$	0	(1.2)
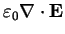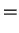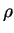$\displaystyle \varepsilon_0 \div\mathbf{E}$	$\displaystyle =$	$\displaystyle \rho$	(1.3)
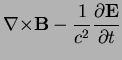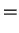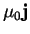$\displaystyle \mathbf{\nabla \times} \mathbf{B}- \frac{1}{c^2} \frac{\partial \mathbf{E}}{\partial t}$	$\displaystyle =$	$\displaystyle \mu_0 \j$	(1.4)

in a shorthand notation where $\bgroup\color{col1}$ \mathbf{B}=\mathbf{B}({\bf r},t)$\egroup$ etc. The transversal parts of $\bgroup\color{col1}$ \mathbf{E}$\egroup$ and $\bgroup\color{col1}$ \mathbf{B}$\egroup$ are dynamical variables:

Subsections

Tobias Brandes 2005-04-26