Gauge Transformations

The potentials are not uniquely determined by the fields which are left invariant under a gauge transformation

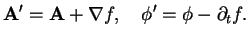$$\mathbf{A}'=\mathbf{A}+ \nabla f,\quad \phi' = \phi -\partial_t f.$$ (1.14)

Again in Fourier space,

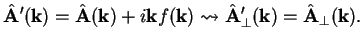$$\hat{\mathbf{A}}'({\bf k})= \hat{\mathbf{A}}({\bf k}) + i {\bf k}... ...k})\leadsto \hat{\mathbf{A}}'_\perp({\bf k}) = \hat{\mathbf{A}}_\perp({\bf k}).$$ (1.15)

The important transverse component of the vector potential, from which the transverse components $\hat{\mathbf{E}}_\perp({\bf k})$ and $\hat{\mathbf{B}}({\bf k})$ are derived via Eq. (VII.1.12), is therefore left invariant under a gauge transformation.