Angular Momentum of Two Particles

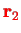If two particles have positions ${\bf r}_1$ and ${\bf r}_2$ and momenta ${\bf p}_1$ and ${\bf p}_2$, the angular momentum of the total system of the two particles is

$${\bf L} = {\bf r}_1 \times {\bf p}_1 + {\bf r}_2 \times {\bf p}_2.$$ (1.1)

We introduce center-of-mass and relative coordinates according to

$${\bf R} = \frac{m_1{\bf r}_1+ m_2{\bf r}_2}{m_1+m_2},\quad {\bf r} = {\bf r}_2-{\bf r}_1,$$ (1.2)

and furthermore momenta

$${\bf P} = {\bf p}_1 + {\bf p}_2$$ (1.3)

$${\bf p} = \frac{m_1{\bf p}_2- m_2{\bf p}_1}{m_1+m_2}.$$ (1.4)

Note that the relative momentum ${\bf p}$ is not just the difference of the individual momenta. It is rather defined such that in terms of

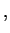$$\mu \equiv \frac{m_1m_2}{m_1+m_2} ,$$ (1.5)

one has

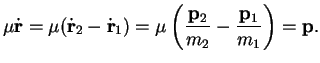$$\mu \dot{\bf r} = \mu (\dot{\bf r}_2 -\dot{\bf r}_1) = \mu \left( \frac{{\bf p}_2}{m_2} -\frac{{\bf p}_1}{m_1} \right) = {\bf p}.$$ (1.6)

Using these definitions, one checks

$${\bf L} = {\bf r}_1 \times {\bf p}_1 + {\bf r}_2 \times {\bf p}_2$$ (1.7)

$$= {\bf R} \times {\bf P} + {\bf r} \times {\bf p}.$$ (1.8)

This is the sum of a center-of-mass angular momentum, ${\bf R} \times {\bf P}$, and a relative angular momentum, ${\bf r} \times {\bf p}$.