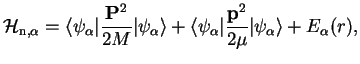Next: Angular Momentum
Up: Hamiltonian
Previous: Angular Momentum of Two
Contents
Index
We recall the Born-Oppenheimer Approximation for the total wave function
 of a molecule, cf. Eq. (V.2.15),
of a molecule, cf. Eq. (V.2.15),
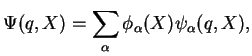 |
|
|
(1.9) |
where
 stands for the electronic,
stands for the electronic,
 for the nuclear coordinates, and the sum is over a complete set of adiabatic electronic eigenstates with electronic quantum numbers
for the nuclear coordinates, and the sum is over a complete set of adiabatic electronic eigenstates with electronic quantum numbers
 . This form leads to the Schrödinger equation in the adiabatic approximation Eq. (V.2.17),
. This form leads to the Schrödinger equation in the adiabatic approximation Eq. (V.2.17),
![$\displaystyle \left[\langle \psi_\alpha\vert \mathcal{H}_{\rm n}\vert\psi_\alph...
...ha(X)\right] \vert\phi_\alpha\rangle_n
= \mathcal{E} \vert\phi_\alpha\rangle_n.$](img1357.png) |
|
|
(1.10) |
Here,
 is the potential acting on the nuclei. We now specify the kinetic energy of the nuclear part for a diatomic molecule,
is the potential acting on the nuclei. We now specify the kinetic energy of the nuclear part for a diatomic molecule,
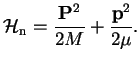 |
|
|
(1.11) |
Exercise Check that
 .
.
The effective nuclear Hamiltonian corresponding to an electronic eigenstate
 thus is
thus is
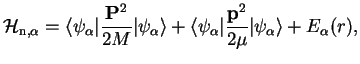 |
|
|
(1.12) |
which is a sum of a center-of-mass Hamiltonian and a Hamiltonian for the relative motion of the two nuclei.
Only the latter is interesting because it contains the potential
 . Note that both
center-of-mass and relative Hamiltonian still contain the geometrical phase terms, cf. Eq. (E.5.2),
which however we will neglect in the following.
. Note that both
center-of-mass and relative Hamiltonian still contain the geometrical phase terms, cf. Eq. (E.5.2),
which however we will neglect in the following.





Next: Angular Momentum
Up: Hamiltonian
Previous: Angular Momentum of Two
Contents
Index
Tobias Brandes
2005-04-26
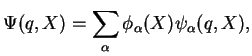
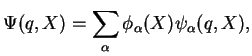
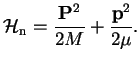
![]() .
.
![]() thus is
thus is