Angular Momentum

Neglecting the geometric phase terms, Eq. (E.5.2), we have in three spatial dimensions

$$\mathcal{H}_{{\rm n},\alpha}^{\rm rel} = \frac{{\bf p}^2}{2\mu} + E_\alpha(r) = - \frac{\hbar^2}{2\mu}\Delta_{\bf r} + E_\alpha(r)$$

$$= - \frac{\hbar^2}{2\mu} \left(\frac{\partial^2}{\partial r^2}+\fra... ...}\frac{\partial}{\partial r}\right) + \frac{{\bf J}^2}{2\mu r^2} + E_\alpha(r),$$ (1.13)

where ${\bf J}$ is the relative angular momentum operator of the nuclei. We have a three-dimensional problem which however due to the radial symmetry of $E_\alpha(r)$ is reduced to a one-dimensional radial eqaution, very much as for the case of the hydrogen atom! We could write the eigenfunctions of $\mathcal{H}_{{\rm n},\alpha}^{\rm rel}$ as

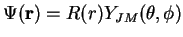$$\Psi({\bf r}) = R(r) Y_{JM}(\theta,\phi)$$ (1.14)

with the corresponding angular quantum numbers $J$ and $M$ of the nuclear relative motion separated off in the spherical harmonics.

Instead of dealing with the angular momentum operator of the nuclei, one would rather descrive rotations of the whole molecule by the total angular momentum ${\bf K}$ of the molecule

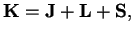$${\bf K} = {\bf J} + {\bf L} + {\bf S},$$ (1.15)

where ${\bf L}$ is the total angular momentum of all electrons and ${\bf S}$ is the total spin.