Next: Pure Rotation
Up: Selection Rules
Previous: Selection Rules
Contents
Index
Assume system of charges
 localised around a spatial position
localised around a spatial position
 .
The coupling to an electric field
.
The coupling to an electric field
 within dipole approximation is then given by
within dipole approximation is then given by
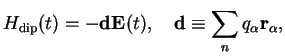 |
|
|
(2.1) |
where
 is the electric field at
is the electric field at
 .
The dipole approximation is valid if the spatial variation of
.
The dipole approximation is valid if the spatial variation of
 around
around
 is
important only on length scales
is
important only on length scales
 with
with
 , where
, where
 is the size of the volume in which the charges are localised. For a plane wave electric field with wave length
is the size of the volume in which the charges are localised. For a plane wave electric field with wave length
 one would have
one would have
 .
.
Tobias Brandes
2005-04-26