Pure Rotation

Pure rotational transitions are between states where only rotational quantum numbers are changed,

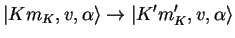$$\vert Km_K, v, \alpha\rangle \to \vert K'm_K', v, \alpha\rangle$$ (2.2)

leaving the vibrational quantum number(s) 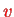$v$ and the electronic quantum number(s) $\alpha$ unchanged. Such transitions then depend on matrix elements of the dipole operator,

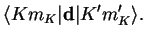$$\langle Km_K\vert {\bf d} \vert K'm_K'\rangle.$$ (2.3)

The calculation of this matrix element, using spherical harmonics, yields the purely rotational selection rules

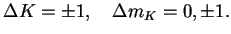$$\Delta K = \pm 1,\quad \Delta m_K = 0,\pm 1.$$ (2.4)

Writing the rotational part of the energy as

$$\varepsilon_{\rm rot}(K) = BK(K+1)$$ (2.5)

$$\leadsto \Delta\varepsilon_{\rm rot}(K)\equiv B(K+1)(K+2) - BK(K+1) = 2B (K+1).$$

The distance between the corresponding spectral lines is constant, $\Delta\varepsilon_{\rm vib}(K+1)-\Delta\varepsilon_{\rm vib}(K)=2B$.