Pure Vibrational Dipole Transitions

Pure vibrational transitions are between states where only vibrational quantum numbers are changed,

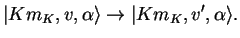$$\vert Km_K, v, \alpha\rangle \to \vert Km_K, v', \alpha\rangle.$$ (2.13)

Such transitions then depend on matrix elements of the dipole operator,

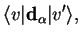$$\langle v\vert {\bf d}_\alpha \vert v'\rangle,$$ (2.14)

where $\vert v\rangle$ is an harmonic oscillator eigenstate (we write 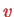$v$ instead of $n$ now), and

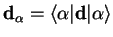$${\bf d}_\alpha = \langle \alpha \vert {\bf d} \vert\alpha\rangle$$ (2.15)

is the diagonal matrix element of the dipole operator between the adiabatic electronic eigenstates $\vert\alpha\rangle$.

Remember that the harmonic potential came from the Taylor expansion of the Born-Oppenheimer energy,

$$U_\alpha(r) \approx U_\alpha(r_\alpha) + \frac{1}{2}\frac{d^2}{dr^2} U_\alpha(r=r_\alpha)(r-r_\alpha)^2$$

$$\leadsto \hat{H}_{\rm osc} = \frac{\hat{p}^2}{2\mu}+\frac{1}{2}m\omega_\alpha^2\hat{x}^2= \hbar\omega_\alpha\left(a^{\dagger}a+\frac{1}{2}\right)$$ (2.16)

$$\omega_\alpha^2 = \frac{1}{\mu} \frac{d^2}{dr^2} U_\alpha(r=r_\alpha)$$ (2.17)

where the harmonic oscillator coordinate $x=r-r_\alpha$.

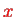The dipole moment operator ${\bf d}_\alpha$ depends on the electronic wave functions $\alpha$ and thus parametrically on the coordinate $x$ that describes the internuclear separation. We Taylor-expand

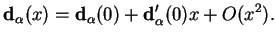$${\bf d}_\alpha(x) = {\bf d}_\alpha(0) + {\bf d}_\alpha'(0) x + O(x^2).$$ (2.18)

For transitions between 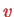$v$ and $v'\ne v$, one therefore has to linear approximation

$$\langle v\vert {\bf d}_\alpha \vert v' \rangle = {\bf d}_\alpha'(0) \langle v\vert x \vert v' \rangle = {\bf d}_\a... ...0)\sqrt{\frac{\hbar}{2\mu\omega}} \langle v\vert a+a^{\dagger} \vert v' \rangle$$

$$= {\bf d}_\alpha'(0)\sqrt{\frac{\hbar}{2\mu\omega}} \left(\delta_{v+1,v'} \sqrt{v+1} + \delta_{v-1,v'} \sqrt{v} \right).$$ (2.19)

The vibrational selection rule thus is

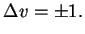$$\Delta v = \pm 1.$$ (2.20)

The corresponding energy differences determine the transition frequency,

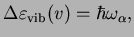$$\Delta \varepsilon_{\rm vib}(v) = \hbar\omega_\alpha,$$ (2.21)

which means that a purely vibrational, harmonic spectrum just consists of a single spectral line!