The -Matrix

Next: Two molecules Up: Effective Interaction between Molecules Previous: From Classical to Quantum Contents Index

The $\bgroup\color{col1}$ T$\egroup$ -Matrix

For the following, Economou's `Green's functions in quantum physics' [11] is a useful reference.

We perform perturbation theory for a Hamiltonian

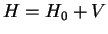$\displaystyle H = H_0 + V$

(2.12)

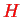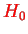by defining two Green's functions (resolvents) of $\bgroup\color{col1}$ H$\egroup$ and $\bgroup\color{col1}$ H_0$\egroup$ as the operators

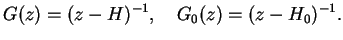$\displaystyle G(z) = (z-H)^{-1},\quad G_0(z) = (z-H_0)^{-1}.$

(2.13)

We have

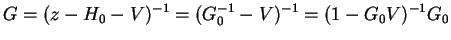$\displaystyle G = (z-H_0-V)^{-1}= (G_0^{-1}-V)^{-1} = (1-G_0V)^{-1} G_0$

(2.14)

and by expanding in $\bgroup\color{col1}$ V$\egroup$ we obtain the Dyson equation

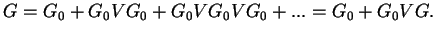$\displaystyle G = G_0 + G_0VG_0 + G_0VG_0VG_0 + ... = G_0 + G_0VG.$

(2.15)

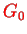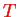We can express the full Green's function $\bgroup\color{col1}$ G$\egroup$ in terms of the free Green's function $\bgroup\color{col1}$ G_0$\egroup$ and the $\bgroup\color{col1}$ T$\egroup$ -matrix,

$\displaystyle G$	$\displaystyle =$	$\displaystyle G_0 + G_0VG_0 + G_0VG_0VG_0 + G_0VG_0VG_0VG_0+...$
	$\displaystyle =$	$\displaystyle G_0 + G_0 \left[ V + VG_0V + VG_0VG_0V + ... \right ]G_0 \equiv G_0 + G_0T G_0$
$\displaystyle T(z)$	$\displaystyle \equiv$	$\displaystyle V + VG_0(z) V + VG_0(z)VG_0(z)V + ...$	(2.16)

We recognize that 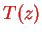$\bgroup\color{col1}$ T(z)$\egroup$ plays the role of an effective, $\bgroup\color{col1}$ z$\egroup$ -dependent potential, the knowledge of which is sufficient to calculate the full Green's function $\bgroup\color{col1}$ G$\egroup$ .

Next: Two molecules Up: Effective Interaction between Molecules Previous: From Classical to Quantum Contents Index

Tobias Brandes 2005-04-26