Two molecules

(Reading assigment: revision of statistical density operator).

We assume the unperturbed state (no interaction) of the two molecules described by a (quantum statistical) density operator

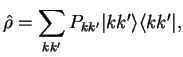$$\hat{\rho} = \sum_{kk'}P_{kk'} \vert kk'\rangle \langle kk'\vert,$$ (2.17)

where the undashed indices refer to molecule 1 and the dashed ones to molecule 2. We call the unperturbed eigenvalues of ${\mathcal H}_0$

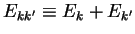$$E_{kk'} \equiv E_k + E_{k'}$$ (2.18)

and define the effective interaction as

$$V_{\rm eff} \equiv \sum_{kk'} p_{kk'} \langle kk'\vert T(E_{kk'}) \vert kk'\rangle$$ (2.19)

$$= \sum_{kk'} P_{kk'} \langle kk'\vert V \vert kk'\rangle + \sum_{kk'} P_{kk'} \langle kk'\vert VG_0(E_{kk'}) V \vert kk'\rangle +...$$

$$\equiv V_{\rm eff}^{(1)} + V_{\rm eff}^{(2)} + ...$$ (2.20)

We write the interaction potential operator $V$

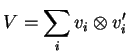$$V = \sum_i v_i \otimes v_i'$$ (2.21)

as a sum over products of operators belonging to molecule 1 and molecule 2. We furthermore assume uncorrelated classical probabilities

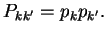$$P_{kk'} = p_k p_{k'}.$$ (2.22)