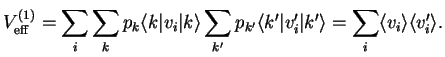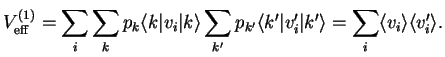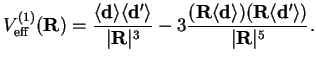Next: Second oder term: (London)
Up: Effective Potentials
Previous: Two molecules
Contents
Index
The first order term in
 in our expansion Eq. (IX.2.20) is
in our expansion Eq. (IX.2.20) is
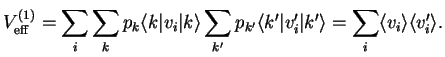 |
|
|
(2.23) |
This is just given by the expectation value of the terms that make up the interaction potential
 , Eq. (IX.2.22).
For the dipole-dipole interaction, this gives
, Eq. (IX.2.22).
For the dipole-dipole interaction, this gives
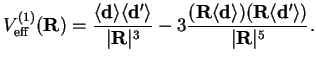 |
|
|
(2.24) |
Since the first order is linear in the interaction potential operator
 , the effective
, the effective
 is essential just the
is essential just the
 with all operators replaced by their expectation values.
This is the static dipole-dipole interaction between the molecules. The corresponding force between the two dipoles is
with all operators replaced by their expectation values.
This is the static dipole-dipole interaction between the molecules. The corresponding force between the two dipoles is
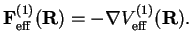 |
|
|
(2.25) |
Its form is just as in the classical dipole-dipole interaction. However, this interaction is zero if one of the expectation values of the dipole moment operators vanishes. Such molecules are said to have no static dipole moment.





Next: Second oder term: (London)
Up: Effective Potentials
Previous: Two molecules
Contents
Index
Tobias Brandes
2005-04-26