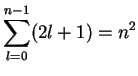Next: A `Mini-Molecule': Perturbation Theory
Up: Hydrogen Atom (non-relativistic)
Previous: Orbital Angular Momentum
Contents
Index
The solutions of Eq. (II.1.7) are now seperated into radial part  and spherical part
and spherical part
 ,
,
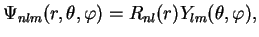 |
|
|
(1.17) |
where radial eigenfunctions for the bound states are characterised by the two integer quantum numbers  and
and  ,
,
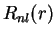 |
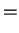 |
![$\displaystyle -\frac{2}{n^2}\sqrt{\frac{(n-l-1)!}{[(n+l)!]^3}}
e^{-Zr/na_0}\lef...
...}{na_0}\right)^lL^{2l+1}_{n+l}\left(\frac{2Zr}{na_0}\right),\quad
l=0,1,...,n-1$](img91.png) |
(1.18) |
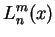 |
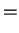 |
 generalized Laguerre polynomials generalized Laguerre polynomials |
|
The radial wave functions  have
have
 nodes.
For these states, the possible eigenvalues only depend on
nodes.
For these states, the possible eigenvalues only depend on
 ,
,
 with
with
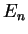 |
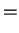 |
 Lyman Formula Lyman Formula |
|
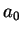 |
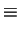 |
 Bohr Radius Bohr Radius |
(1.19) |
In Dirac notation, we write the stationary states as
 with the correspondence
with the correspondence
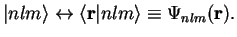 |
|
|
(1.20) |
The ground state is
 with energy
with energy
 eV. The degree of degeneracy of the energy level
eV. The degree of degeneracy of the energy level
 , i.e. the number of linearly independent stationary states with quantum number
, i.e. the number of linearly independent stationary states with quantum number
 , is
, is
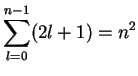 |
|
|
(1.21) |
Backup literature: lecture notes QM 1
http://brandes.phy.umist.ac.uk/QM/http://brandes.phy.umist.ac.uk/QM/, textbooks Merzbacher [2], Landau-Lifshitz III [1], Gasiorowisz [3].





Next: A `Mini-Molecule': Perturbation Theory
Up: Hydrogen Atom (non-relativistic)
Previous: Orbital Angular Momentum
Contents
Index
Tobias Brandes
2005-04-26
![$\displaystyle -\frac{2}{n^2}\sqrt{\frac{(n-l-1)!}{[(n+l)!]^3}}
e^{-Zr/na_0}\lef...
...}{na_0}\right)^lL^{2l+1}_{n+l}\left(\frac{2Zr}{na_0}\right),\quad
l=0,1,...,n-1$](img91.png)
 generalized Laguerre polynomials
generalized Laguerre polynomials Lyman Formula
Lyman Formula Bohr Radius
Bohr Radius