




Next: .
Up: Time-Dependence
Previous: Time-Dependence
Contents
Index
Consider the Hamiltonian for a particle in a double well potential with both energies left and right
 and tunnel coupling
and tunnel coupling
 ,
,
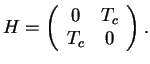 |
|
|
(6.1) |
Consider an initial state at time
 ,
,
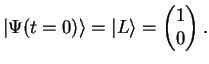 |
|
|
(6.2) |
a) Calculate the state vector
 for times
for times
 .
.
b) Use the result from a) to calculate the probability to find the particle in the left well after time
 .
.
Tobias Brandes
2005-04-26
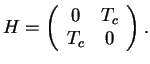
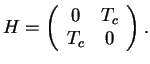
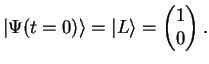
 for times
for times
![]() .
.
![]() .
.