




Next: Degenerate Perturbation Theory for
Up: Perturbation Theory for Fine
Previous: Perturbation Theory for Fine
Contents
Index
Assume a
 -fold degenerate energy level
-fold degenerate energy level
 with
with
 degenerate eigenstates of
degenerate eigenstates of
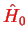
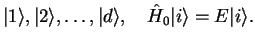 |
|
|
(3.16) |
The perturbation
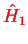 leads to new eigenfunctions
leads to new eigenfunctions
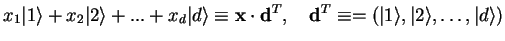 |
|
|
(3.17) |
where the notation
 is just an abbreviation using the coefficient vector
is just an abbreviation using the coefficient vector
 and
the vector of the degenerate states
and
the vector of the degenerate states
 . The coefficient vectors
. The coefficient vectors
 are then determined from the matrix eigenvalue equation
are then determined from the matrix eigenvalue equation
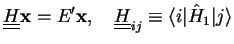 |
|
|
(3.18) |
with the Hermitian
 times
times
 matrix
matrix
 of the matrix elements of the perturbation
of the matrix elements of the perturbation
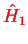 in the sub-space of the degenerate eigenstates
in the sub-space of the degenerate eigenstates
 of
of
 .
.
The solutions for
 are determined from
are determined from
 or
or
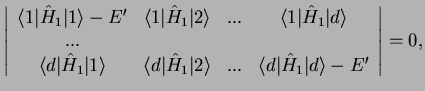 |
|
|
(3.19) |
which is an algebraic equation with
 real solutions
real solutions
 ,
,
 . Correspondingly, one obtains
. Correspondingly, one obtains
 coefficient vectors
coefficient vectors
 leading to
leading to
 new linear combinations
new linear combinations
 ,
,
 , of states within the
, of states within the
 -dimensional subspace spanned by
-dimensional subspace spanned by
 .
.
Exercise 1: Revise if necessary Gasiorowicz [3] cp. 11.2, plus the corresponding math background: eigenvalues, eigenvalue equations, vector spaces, matrices etc. !
Exercise 2: Revise degenerate perturbation theory by applying it to the 2-level system
 from section II.2 for the case
from section II.2 for the case
 . How good is first order perturbation theory in this case?
. How good is first order perturbation theory in this case?





Next: Degenerate Perturbation Theory for
Up: Perturbation Theory for Fine
Previous: Perturbation Theory for Fine
Contents
Index
Tobias Brandes
2005-04-26
![]() are determined from
are determined from
![]() or
or
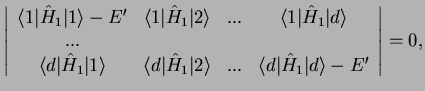
![]() from section II.2 for the case
from section II.2 for the case
![]() . How good is first order perturbation theory in this case?
. How good is first order perturbation theory in this case?