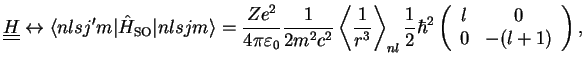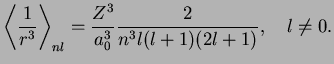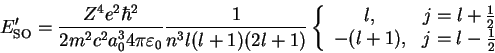Next: Putting everything together
Up: Perturbation Theory for Fine
Previous: Degenerate Perturbation Theory
Contents
Index
Including spin, the level
 of hydrogen belongs to the states
of hydrogen belongs to the states
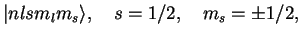 |
|
|
(3.20) |
which are eigenstates of
 ,
,
 ,
,
 , and
, and
 (`uncoupled representation').
With
(`uncoupled representation').
With
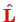 and
and
 adding up to the total angular momentum
adding up to the total angular momentum
 , an alternative basis is the `coupled representation'
, an alternative basis is the `coupled representation'
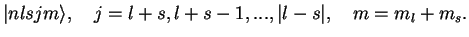 |
|
|
(3.21) |
of eigenfunctions of
 ,
,
 ,
,
 , and
, and
 . Here,
. Here,
 is the total electron spin which of course is fixed and gives the two possibilities
is the total electron spin which of course is fixed and gives the two possibilities
 and
and
 for
for
 and
and
 for
for
 (
(
 runs from
0 to
runs from
0 to
 ).
).
The perturbation
 , Eq. (II.3.12), can be diagonalised in the
, Eq. (II.3.12), can be diagonalised in the
 basis, using
basis, using
For fixed
 ,
,
 , and
, and
 , (
, (
 is fixed anyway and therefore a dummy index), the basis of degenerate states from the previous subsection therefore for
is fixed anyway and therefore a dummy index), the basis of degenerate states from the previous subsection therefore for
 has two states,
has two states,
 , and the two-by-two matrix
, and the two-by-two matrix
 is diagonal,
is diagonal,
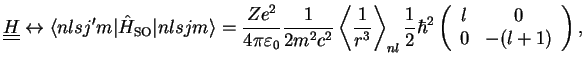 |
|
|
(3.23) |
where
 indicates that this matrix elements has to be calculated with the radial parts of the wave functions
indicates that this matrix elements has to be calculated with the radial parts of the wave functions
 , with the result
, with the result
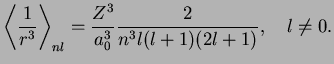 |
|
|
(3.24) |
The resulting energy shifts
 corresponding to the two states with
corresponding to the two states with
 are
are
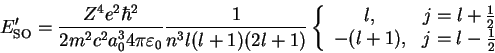 |
|
|
(3.25) |





Next: Putting everything together
Up: Perturbation Theory for Fine
Previous: Degenerate Perturbation Theory
Contents
Index
Tobias Brandes
2005-04-26
![]() , Eq. (II.3.12), can be diagonalised in the
, Eq. (II.3.12), can be diagonalised in the
![]() basis, using
basis, using