Total Spin

One advantage of working with singlets and triplets is the fact that they are spin states of fixed total spin: rthe singlets has total spin 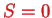$S=0$, the three triplets have total spin 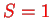$S=1$ and total spin projections $M=-1,0,1$:

$$\hat{S}^2 \vert S\rangle = \hbar S(S+1) \vert S\rangle, S=0,\quad \hat{S}_z \vert S\rangle = \hbar M \vert S\rangle, M=0$$ (2.14)

$$\hat{S}^2 \vert T_{-1}\rangle = \hbar S(S+1) \vert T_{-1}\rangle, S=1,\quad \hat{S}_z \vert T_{-1}\rangle = \hbar M \vert T_{-1}\rangle, M=-1$$

$$\hat{S}^2 \vert T_{0}\rangle = \hbar S(S+1) \vert T_{0}\rangle, S=1,\quad \hat{S}_z \vert T_{0}\rangle = \hbar M \vert T_{0}\rangle, M=0$$

$$\hat{S}^2 \vert T_{+1}\rangle = \hbar S(S+1) \vert T_{+1}\rangle, S=1,\quad \hat{S}_z \vert T_{+1}\rangle = \hbar M \vert T_{+1}\rangle, M=+1.$$

Often the total spin is conserved when we deal with interacting systems. If , for example, the system is in a state that is a linear combination of the three triplets, it has to stay in the sub-space spanned by the triplets and can't get out of it. In that case instead of having a four-dimensional space we just have to deal with a three-dimensional space.