Entanglement

There is a fundamental difference between the $M=\pm 1$ states $\vert T_{\pm 1}\rangle$ on the one side and the $M=0$ states $\vert S\rangle$ and $\vert T_0\rangle$ on the other side:

• $\vert T_{-1}\rangle = \vert\downarrow \rangle_1 \otimes \vert\downarrow \rangle_2$ and $\vert T_{+1}\rangle = \vert\uparrow \rangle_1 \otimes \vert\uparrow \rangle_2$ are product states.
• $\vert S\rangle = \frac{1}{\sqrt{2}}\left[ \vert\uparrow \rangle_1 \otimes \ve... ...olor{col1}-} \vert\downarrow \rangle_1 \otimes \vert\uparrow \rangle_2 \right]$ and $\vert T_0\rangle = \frac{1}{\sqrt{2}}\left[ \vert\uparrow \rangle_1 \otimes \v... ...color{col1}+} \vert\downarrow \rangle_1 \otimes \vert\uparrow \rangle_2 \right]$ can not be written as product states: they are called entangled states.

For product states of two particles 1 and 2 (pure tensors),

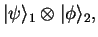$$\vert\psi\rangle_1 \otimes \vert\phi\rangle_2,$$ (2.15)

one can say that particle 1 is in state $\vert\psi\rangle$ and particle 2 is in state $\vert\phi\rangle$. States that can not be written as product states are called entangled states. For example, for the state

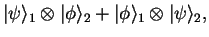$$\vert\psi\rangle_1 \otimes \vert\phi\rangle_2 + \vert\phi\rangle_1 \otimes \vert\psi\rangle_2,$$ (2.16)

one can not say which particle is in which state: the two particles are entangled. Entanglement is the key concept underlying all modern quantum information theory, such as quantum cryptography, quantum teleportation, or quantum computing.