The Variational Principle

The stationary Schrödinger equation

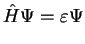$$\hat{H}\Psi = \varepsilon \Psi$$ (3.1)

can be derived from a variational principle. For the ground state of the system, this is formulated as a problem of finding the wave vector $\Psi$ of the system among all possible wave vectors such that the expectation value of the energy (i.e., the Hamiltonian) is minimized,

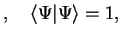$$\langle \Psi\vert \hat{H} \vert \Psi \rangle = ,\quad \langle \Psi \vert \Psi\rangle =1,$$ (3.2)

under the additional condition that $\Psi$ be normalised. We are therefore looking for a minimum of the energy functional

$$E[\Psi]\equiv \langle \Psi\vert \hat{H} \vert \Psi \rangle$$ (3.3)

under the additional condition that $\Psi$ be normalised.