Lagrange Multiplier

The additional condition $\langle \Psi \vert \Psi\rangle =1$ can be incorporated into the minimisation procedure by adding a term to the energy functional, introducing a Lagrange multiplier $\lambda$, and thereby defining the functional

$$F[\Psi] \equiv E[\Psi] + \lambda \left[\langle \Psi \vert \Psi \rangle-1\right].$$ (3.8)

Its functional derivative is

$$\frac{\delta F[\Psi]}{\delta \Psi} = \langle \delta \Psi\vert \hat{H}\vert \Psi \rangle + \langle \Psi... ... \delta \Psi \vert \Psi \rangle + \langle \Psi\vert \delta \Psi \rangle\right].$$ (3.9)

Exercise: Check this equation.

Minimization then means

$$0= \frac{\delta F[\Psi]}{\delta \Psi}\leadsto \langle \delta \Psi... ... \Psi \rangle + \langle \Psi\vert \hat{H}+\lambda\vert \delta \Psi \rangle = 0.$$ (3.10)

As $\delta \Psi$ is arbitrary and complex, this can only be true if

$$[\hat{H}+\lambda]\vert \Psi \rangle =0,\quad \langle \Psi\vert [\hat{H}+\lambda]=0$$ (3.11)

which are two equations which are the conjugate complex to each other. Writing $\lambda=-\varepsilon$, this means

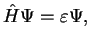$$\hat{H} \Psi = \varepsilon\Psi,$$ (3.12)

which is the stationary Schrödinger equation. However, here $\varepsilon$ is the lowest eigenvalue with corresponding eigenstate $\Psi$. We thus recognise:

Minimization of the functional $F[\Psi] \equiv E[\Psi] -\varepsilon \left[\langle \Psi \vert \Psi \rangle-1\right]$ is equivalent to finding the lowest eigenvalue and eigenstate of the stationary Schrödinger equation $\hat{H}\Psi=\varepsilon\Psi$.