Example: $N=2$, `closed shell'

In the case $N=2$, we are back to the Helium atom ( $N=2$ electrons). We assume

$$\psi_{\nu_{1}}({\bf r},\sigma) = \psi ({\bf r})\vert\uparrow \rangle,\quad \psi_{\nu_{2}}({\bf r},\sigma) = \psi ({\bf r})\vert\downarrow \rangle,$$ (3.32)

i.e. we only have two spin orbitals with opposite spin. From the Hartree-Fock equations Eq. (E.4.2), we obtain

$$\left[ \hat{H_0} + {\sum_{i=1}^2 \int d{\bf r'} \vert\psi({\bf r'})\vert^2 U(\vert{r-r'}\vert)} \right] \psi({\bf r})$$

$$- {\sum_{i=1}^2 \int d{\bf r'} \psi^*({\bf r'}) U(\vert{r-r'}\vert) \psi({\bf r'}) \psi({\bf r}) \delta_{\sigma_i \sigma_j}} = \varepsilon_j \psi({\bf r}) .$$ (3.33)

Formally, these are still two equations due to the label $j$ ( $=1,2$), but the two equations are the same and we may set $\varepsilon_1=\varepsilon_2=\varepsilon$. The sum in the exchange part has only one term which is half the direct part, and therefore (we re-insert the explicit expression for $\hat{H}_0$)

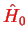$$\left[ -\frac{\hbar^2}{2m}\Delta + V({\bf r}) + \int d{\bf r'} \v... ...})\vert^2 U(\vert{r-r'}\vert) \right] \psi({\bf r})= \varepsilon \psi({\bf r}).$$ (3.34)

Since we have only one orbital wave function, we only have one equation.