




Next: Bonding and Antibonding
Up: The Hydrogen Molecule Ion
Previous: Hamiltonian for
Contents
Index
For a given Hamiltonian
 we minimise the expectation value of the energy over a sub-set of states
we minimise the expectation value of the energy over a sub-set of states
 that are linear combinations of
that are linear combinations of
 given states
given states
 ,
,
The
 are assumed to be normalised but not necessarily mutually orthogonal, i.e., one can have
are assumed to be normalised but not necessarily mutually orthogonal, i.e., one can have
 .
.
The energy
 is therefore minimized with respect to the
is therefore minimized with respect to the
 coefficients
coefficients
 ,
,
 . It can be written as
. It can be written as
where one has introduced the matrices
 and
and
 with matrix elements
with matrix elements
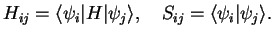 |
|
|
(3.4) |
We find the minimum of
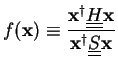 |
|
|
(3.5) |
by setting the gradient to zero. We treat
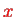 and its complex conjugate
and its complex conjugate
 as independent variables and calculate
as independent variables and calculate
Correspondingly,
Thus,
since
 at the minimum! A necessary condition for a minimum therefore is the equation
at the minimum! A necessary condition for a minimum therefore is the equation
 , which has a solution for
, which has a solution for
 only if
only if
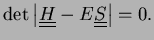 |
|
|
(3.9) |
Exercise: Check which equations one obtains when taking the derivative
 instead of
instead of
 !
!
We summarise:
The minimization problem thus led us to an eigenvalue problem.





Next: Bonding and Antibonding
Up: The Hydrogen Molecule Ion
Previous: Hamiltonian for
Contents
Index
Tobias Brandes
2005-04-26
![]() we minimise the expectation value of the energy over a sub-set of states
we minimise the expectation value of the energy over a sub-set of states
![]() that are linear combinations of
that are linear combinations of
![]() given states
given states
![]() ,
,

![]() is therefore minimized with respect to the
is therefore minimized with respect to the
![]() coefficients
coefficients
![]() ,
,
![]() . It can be written as
. It can be written as
 min
min
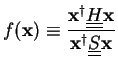



![]() instead of
instead of
![]() !
!
