




Next: Roothan Equations
Up: Molecules
Previous: Molecular Potential Energy
Contents
Index
We now discuss a method to calculate molecular orbitals within the Hartree-Fock method. Let us start from Eq. (IV.3.27),
and assume a closed shell situation and a Hamiltonian
 which is diagonal in spin-space, i.e. does not flip the spin. The counter
which is diagonal in spin-space, i.e. does not flip the spin. The counter
 runs from
runs from
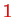 to
to
 , there are
, there are
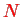 orbitals with spin up and
orbitals with spin up and
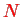 orbitals with spin down. The index
orbitals with spin down. The index
 thus runs like
thus runs like
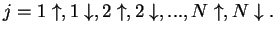 |
|
|
(4.2) |
We write
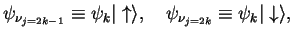 |
|
|
(4.3) |
because
 ,
,
 corresponds to spin-orbitals with spin
corresponds to spin-orbitals with spin
 and
and
 ,
,
 corresponds to spin-orbitals with spin
corresponds to spin-orbitals with spin
 .
Use the Fock operator
.
Use the Fock operator
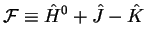 |
|
|
(4.4) |
and let us, for example, set
 to obtain
to obtain
and expand the orbital wave function as
with
 given atomic orbitals.
Inserting yields
given atomic orbitals.
Inserting yields
Subsections





Next: Roothan Equations
Up: Molecules
Previous: Molecular Potential Energy
Contents
Index
Tobias Brandes
2005-04-26




 LCAO
LCAO