Hartree-Fock for Molecules

We now discuss a method to calculate molecular orbitals within the Hartree-Fock method. Let us start from Eq. (IV.3.27),

$$\left(\hat{H^0} + \hat{J}-\hat{K}\right)\vert \nu_{j}\rangle = \varepsilon_j\vert \nu_{j}\rangle$$ (4.1)

$$\langle \mu \vert\hat{J} \vert\nu_j\rangle \equiv \sum_i\langle \mu \nu_i \vert U \vert\nu_i \nu_j\rangle,\quad \la... ...ert\nu_j\rangle \equiv \sum_i\langle \mu \nu_i \vert U \vert\nu_j \nu_i\rangle,$$

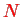and assume a closed shell situation and a Hamiltonian $\hat{H^0}+U$ which is diagonal in spin-space, i.e. does not flip the spin. The counter $j$ runs from $1$ to $2N$, there are $N$ orbitals with spin up and 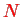$N$ orbitals with spin down. The index $j$ thus runs like

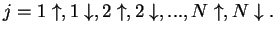$$j=1\uparrow,1\downarrow,2\uparrow,2\downarrow,...,N\uparrow,N\downarrow.$$ (4.2)

We write

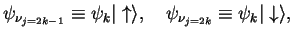$$\psi_{\nu_{j=2k-1}} \equiv \psi_k \vert\uparrow\rangle,\quad \psi_{\nu_{j=2k}} \equiv \psi_k \vert\downarrow\rangle,$$ (4.3)

because $j=2k$, $k=1,...,N$ corresponds to spin-orbitals with spin $\downarrow$ and $j=2k-1$, $k=1,...,N$ corresponds to spin-orbitals with spin $\uparrow$. Use the Fock operator

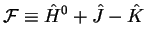$${\mathcal F} \equiv \hat{H}^0 + \hat{J}-\hat{K}$$ (4.4)

and let us, for example, set $j=2k-1$ to obtain

$${\mathcal F} \vert \psi_{k}\rangle \otimes \vert\uparrow\rangle = \varepsilon_{k\uparrow} \vert\psi_{k}\rangle\otimes \vert\uparrow \rangle$$ (4.5)

and expand the orbital wave function as

$$( )\quad \psi_{k} = \sum_{l=1}^M c_{lk} \phi_l,\quad ( )$$ (4.6)

with $l=1,...,M$ given atomic orbitals. Inserting yields

$$\langle \uparrow \vert\otimes \langle \phi_{l'}\vert {\mathcal F} \vert \sum_{l=1}^M c_{lk} \vert\phi_{l}\rangle \otimes \vert\uparrow\rangle = \varepsilon_{k\uparrow} \sum_{l=1}^M c_{lk} \langle \phi_{l'}\vert \phi_l \rangle$$

$$\sum_{l=1}^M{\mathcal F}^{\uparrow\uparrow}_{l'l} c_{lk} = \varepsilon_{k\uparrow} \sum_{l=1}^M S_{l'l}c_{lk}$$ (4.7)

$$S_{l'l}\equiv \langle \phi_{l'}\vert \phi_l \rangle,\quad {\mathcal F}^{\uparrow\uparrow}_{l'l} \equiv \langle \uparrow \vert\otimes \langle \phi_{l'}\vert {\mathcal F}\vert\phi_{l}\rangle \otimes \vert\uparrow\rangle.$$