Roothan Equations

The equations Eq. (V.4.8) are called Roothan equations (they are usually written for spin-independent Fock-operator ${\mathcal F}$. We summarize the situation so far:

• We have $l=1,...,M$ atomic orbitals (AOs) $\phi_l$ for $k=1,...,N$ molecular orbitals (MOs) expressed as linear combinations (LCAO) of the AOs.
• We define the matrix $\underline{\underline{C}}$ as the matrix of the coefficients, $\underline{\underline{C}}_{lk}=c_{lk}$, $\underline{\underline{S}}$ as the matrix of the overlaps, $\underline{\underline{S}}_{lk}=S_{lk}$, and $\underline{\underline{\mathcal F}}$ as the Fock matrix.
• As $\hat{H^0}+U$ is diagonal in spin-space so is the Fock-operator ${\mathcal F}$ whence there are no mixed terms ${\mathcal F}^{\downarrow\uparrow}$ or ${\mathcal F}^{\uparrow\downarrow}$.

We can then write the Roothan equations as

$$\underline{\underline{\mathcal F}}^{\uparrow\uparrow}\underline{\underline{C}} = \underline{\underline{S}} \underline{\underline{C}} \underline {\underline{\varepsilon}}^{\uparrow}$$ (4.8)

$$\underline{\underline{\mathcal F}}^{\downarrow\downarrow}\underline{\underline{C}} = \underline{\underline{S}} \underline{\underline{C}} \underline{\underline{\varepsilon}}^{\downarrow},$$ (4.9)

where $\underline{\underline{\varepsilon}}$ are diagonal matrices for the energies $\varepsilon_k$. Now these look like simultaneous linear equations but of course they are not, because the Fock-operator depends on the coefficients $c_{kl}$ that we try to determine: recall ${\mathcal F} \equiv \hat{H}^0 + \hat{J}-\hat{K}$ with

$$\hat{J}^{\uparrow\uparrow}_{l'l} \equiv \sum_{i=1}^{2N}\langle l'\nu_i \vert U \vert\nu_i l\rangle$$ (4.10)

$$\hat{K}^{\uparrow\uparrow}_{l'l} \equiv \sum_{i=1}^{2N}\langle l'\nu_i \vert U \vert l \nu_i\rangle \langle \sigma_i\vert\uparrow\rangle ,$$

where we first considered spin up. The $i$-sum runs over spin-orbitals, i.e. AOs including the spin. We now assume $U$ to be spin-independent.

$$\hat{J}_{l'l} \equiv \sum_{\sigma=0,1}\sum_{k=1}^N\langle l' \nu_{2k-\sigma} \vert U \... ...igma} l\rangle = 2 \sum_{k=1}^N \langle l' \psi_k \vert U \vert \psi_k l\rangle$$

$$\hat{K}_{l'l} \equiv \sum_{\sigma=0,1}\sum_{k=1}^N \langle l' \nu_{2k-\sigma} \vert U ... ...uparrow\rangle =\sum_{k=1}^N \langle l' \psi_k \vert U \vert l \psi_k \rangle ,$$

where $\sigma=0$ corresponds to spin down and $\sigma=1$ corresponds to spin up, and the orbital part of the spin-orbital $\nu_{2k-\sigma}$ is $\psi_k$ by definition. Now everything is expressed in terms of orbitals only and the spin has just led to the factor of two in front of the direct term!

We now use the LCAO expansion $\psi_{k}=\sum_m c_{mk}\psi_m$ and thus obtain

$$\hat{J}_{l'l} = 2 \sum_{k=1}^N \sum_{m,m'=1}^M c_{m'k}^*c_{mk} \langle l' m' \ver... ...\vert m l\rangle = \sum_{m,m'=1}^MP_{m'm}\langle l' m' \vert U \vert m l\rangle$$

$$\hat{K}_{l'l} = \phantom{2}\sum_{k=1}^N \sum_{m,m'=1}^M c_{m'k}^*c_{mk} \langle l... ...ngle =\frac{1}{2}\sum_{m,m'=1}^M P_{m'm}\langle l' m' \vert U \vert l m \rangle$$

$$P_{m'm} \equiv 2\sum_{k=1}^N c_{m'k}^*c_{mk},$$ (4.11)

where the populations depend on the 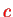$c$'s: it is them who are responsible for the non-linearity (self-consistent character) of the Roothan equations. Summarizing, the matrix elements of the Fock operator are given by

$${\mathcal F}^{\uparrow\uparrow}_{l'l} = \left(\hat{H^0}\right)^{\uparrow\uparrow}_{l'l}$$ (4.12)

$$+ \sum_{m,m'=1}^M P_{m'm}[\{c_{ij}\}] \left( \langle l' m' \vert U \vert m l\rangle -\frac{1}{2} \langle l' m' \vert U \vert l m \rangle\right).$$